|
| 1 | +# 1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance |
| 2 | + |
| 3 | +- Difficulty: Medium. |
| 4 | +- Related Topics: Dynamic Programming, Graph, Shortest Path. |
| 5 | +- Similar Questions: Second Minimum Time to Reach Destination. |
| 6 | + |
| 7 | +## Problem |
| 8 | + |
| 9 | +There are `n` cities numbered from `0` to `n-1`. Given the array `edges` where `edges[i] = [fromi, toi, weighti]` represents a bidirectional and weighted edge between cities `fromi` and `toi`, and given the integer `distanceThreshold`. |
| 10 | + |
| 11 | +Return the city with the smallest number of cities that are reachable through some path and whose distance is **at most** `distanceThreshold`, If there are multiple such cities, return the city with the greatest number. |
| 12 | + |
| 13 | +Notice that the distance of a path connecting cities ****i**** and ****j**** is equal to the sum of the edges' weights along that path. |
| 14 | + |
| 15 | + |
| 16 | +Example 1: |
| 17 | + |
| 18 | +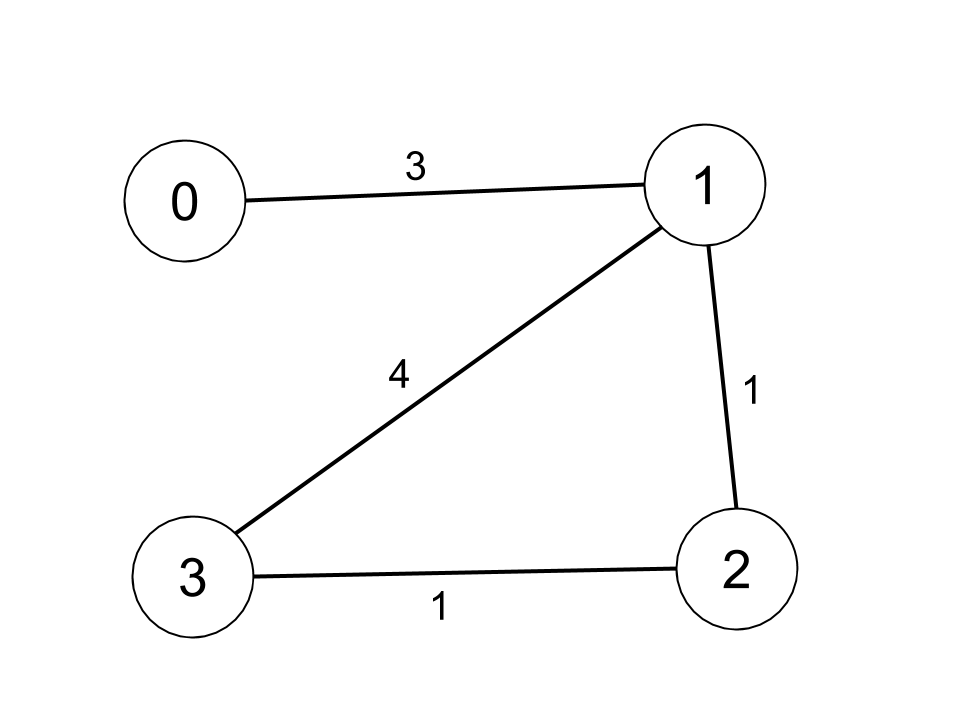 |
| 19 | + |
| 20 | +``` |
| 21 | +Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4 |
| 22 | +Output: 3 |
| 23 | +Explanation: The figure above describes the graph. |
| 24 | +The neighboring cities at a distanceThreshold = 4 for each city are: |
| 25 | +City 0 -> [City 1, City 2] |
| 26 | +City 1 -> [City 0, City 2, City 3] |
| 27 | +City 2 -> [City 0, City 1, City 3] |
| 28 | +City 3 -> [City 1, City 2] |
| 29 | +Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number. |
| 30 | +``` |
| 31 | + |
| 32 | +Example 2: |
| 33 | + |
| 34 | +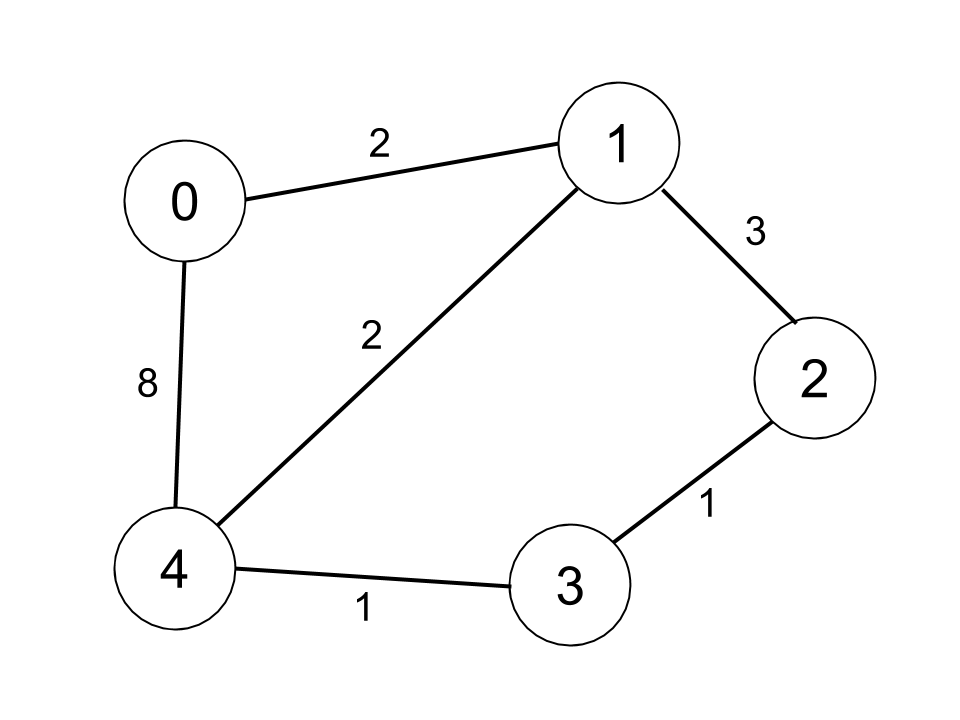 |
| 35 | + |
| 36 | +``` |
| 37 | +Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2 |
| 38 | +Output: 0 |
| 39 | +Explanation: The figure above describes the graph. |
| 40 | +The neighboring cities at a distanceThreshold = 2 for each city are: |
| 41 | +City 0 -> [City 1] |
| 42 | +City 1 -> [City 0, City 4] |
| 43 | +City 2 -> [City 3, City 4] |
| 44 | +City 3 -> [City 2, City 4] |
| 45 | +City 4 -> [City 1, City 2, City 3] |
| 46 | +The city 0 has 1 neighboring city at a distanceThreshold = 2. |
| 47 | +``` |
| 48 | + |
| 49 | + |
| 50 | +**Constraints:** |
| 51 | + |
| 52 | + |
| 53 | + |
| 54 | +- `2 <= n <= 100` |
| 55 | + |
| 56 | +- `1 <= edges.length <= n * (n - 1) / 2` |
| 57 | + |
| 58 | +- `edges[i].length == 3` |
| 59 | + |
| 60 | +- `0 <= fromi < toi < n` |
| 61 | + |
| 62 | +- `1 <= weighti, distanceThreshold <= 10^4` |
| 63 | + |
| 64 | +- All pairs `(fromi, toi)` are distinct. |
| 65 | + |
| 66 | + |
| 67 | + |
| 68 | +## Solution |
| 69 | + |
| 70 | +```javascript |
| 71 | +/** |
| 72 | + * @param {number} n |
| 73 | + * @param {number[][]} edges |
| 74 | + * @param {number} distanceThreshold |
| 75 | + * @return {number} |
| 76 | + */ |
| 77 | +var findTheCity = function(n, edges, distanceThreshold) { |
| 78 | + var map = {}; |
| 79 | + for (var i = 0; i < edges.length; i++) { |
| 80 | + map[edges[i][0]] = map[edges[i][0]] || {}; |
| 81 | + map[edges[i][1]] = map[edges[i][1]] || {}; |
| 82 | + map[edges[i][1]][edges[i][0]] = edges[i][2]; |
| 83 | + map[edges[i][0]][edges[i][1]] = edges[i][2]; |
| 84 | + } |
| 85 | + var min = Number.MAX_SAFE_INTEGER; |
| 86 | + var minNum = -1; |
| 87 | + for (var j = 0; j < n; j++) { |
| 88 | + var cities = dijkstra(j, map, distanceThreshold); |
| 89 | + if (cities <= min) { |
| 90 | + min = cities; |
| 91 | + minNum = j; |
| 92 | + } |
| 93 | + } |
| 94 | + return minNum; |
| 95 | +}; |
| 96 | + |
| 97 | +var dijkstra = function(n, map, distanceThreshold) { |
| 98 | + var visited = {}; |
| 99 | + var queue = new MinPriorityQueue(); |
| 100 | + queue.enqueue(n, 0); |
| 101 | + while (queue.size() > 0) { |
| 102 | + var { element, priority } = queue.dequeue(); |
| 103 | + if (priority > distanceThreshold) break; |
| 104 | + if (visited[element]) continue; |
| 105 | + visited[element] = true; |
| 106 | + var arr = Object.keys(map[element] || {}); |
| 107 | + for (var i = 0; i < arr.length; i++) { |
| 108 | + if (visited[arr[i]]) continue; |
| 109 | + queue.enqueue(arr[i], priority + map[element][arr[i]]); |
| 110 | + } |
| 111 | + } |
| 112 | + return Object.keys(visited).length; |
| 113 | +}; |
| 114 | +``` |
| 115 | + |
| 116 | +**Explain:** |
| 117 | + |
| 118 | +nope. |
| 119 | + |
| 120 | +**Complexity:** |
| 121 | + |
| 122 | +* Time complexity : O(n ^ 3 * log(n)). |
| 123 | +* Space complexity : O(n ^ 2). |
0 commit comments