Abstract
The study is the first to analyze genetic and environmental factors that affect brain fiber architecture and its genetic linkage with cognitive function. We assessed white matter integrity voxelwise using diffusion tensor imaging at high magnetic field (4 Tesla), in 92 identical and fraternal twins. White matter integrity, quantified using fractional anisotropy (FA), was used to fit structural equation models (SEM) at each point in the brain, generating three-dimensional maps of heritability. We visualized the anatomical profile of correlations between white matter integrity and full-scale, verbal, and performance intelligence quotients (FIQ, VIQ, and PIQ). White matter integrity (FA) was under strong genetic control and was highly heritable in bilateral frontal (a2 = 0.55, p = 0.04, left; a2 = 0.74, p = 0.006, right), bilateral parietal (a2 = 0.85, p < 0.001, left; a2 = 0.84, p < 0.001, right), and left occipital (a2 = 0.76, p = 0.003) lobes, and was correlated with FIQ and PIQ in the cingulum, optic radiations, superior fronto-occipital fasciculus, internal capsule, callosal isthmus, and the corona radiata (p = 0.04 for FIQ and p = 0.01 for PIQ, corrected for multiple comparisons). In a cross-trait mapping approach, common genetic factors mediated the correlation between IQ and white matter integrity, suggesting a common physiological mechanism for both, and common genetic determination. These genetic brain maps reveal heritable aspects of white matter integrity and should expedite the discovery of single-nucleotide polymorphisms affecting fiber connectivity and cognition.
Keywords: genetics, cognition, twins, white matter, diffusion imaging, structural equations
Introduction
Identification of genes and environmental factors affecting brain white matter integrity is of fundamental importance in neuroscience. Fiber architecture develops according to an overall genetic program in utero, but neurochemical and environmental cues affect the ultimate pattern of neuronal connectivity, with critical periods for certain environmental inputs (Wiesel and Hubel, 1963). Synaptic connectivity, dendritic complexity and myelination vary dynamically throughout life, responding to sensory stimulation or deprivation, nutritional factors and rearing environment. A key step in understanding the determinants of white matter integrity is to find quantifiable measures of white matter integrity in the brain that are related to cognition.
Diffusion tensor imaging (DTI) is a variant of magnetic resonance imaging that measures directional profiles of water diffusion at each point in the brain (Le Bihan et al., 2001). The fractional anisotropy (FA; or directional variability) of diffusion is higher in heavily myelinated fiber tracts, and increases with progressive myelination during development. Increases in myelination and larger axonal diameter have been associated with increased neuronal conduction speed and may support better cognitive function (Aboitiz, 1992; Jung and Haier, 2007). FA correlates with intellectual performance in normal subjects (Yu et al., 2008), and is reduced by degenerative processes that impair axonal fiber integrity (Choi et al., 2005).
Several measures of brain morphometry are under strong genetic control, including regional gray and white matter volumes (Hulshoff Pol et al., 2006) and cortical thickness (Schmitt et al., 2008a,b; Lenroot et al., 2009). Total brain volume is correlated with intelligence quotient [IQ; r ∼0.33 in a meta-analysis of 1530 subjects (McDaniel, 2005)] and the same set of genes influences both IQ and gray/white matter volumes (Posthuma et al., 2002). Only one diffusion imaging study has examined white matter integrity in twins (Pfefferbaum et al., 2001); that study suggested strong genetic influences, but regions of interest were limited to the midsagittal corpus callosum.
In this study, we performed an observational exploratory study by scanning 92 genetically identical and fraternal twins (23 pairs of each) using DTI, to estimate the relative contribution of genetics and environment to white matter integrity, and detect the connection between the genetics of white matter integrity and intelligence. We applied an innovative information-theoretic measure, the symmetrized Kullback–Leibler divergence of the two tensor-valued images, to register DTI. We examined correlations between identical and fraternal twins, by fitting quantitative genetic models at each location in the brain (Neale et al., 1992), creating spatially detailed maps of genetic and environmental influences on white matter integrity. We found that brain architecture was under strong genetic control. White matter integrity was linked with intellectual performance, especially with performance IQ; this linkage was found to be primarily mediated by common genetic influences.
Materials and Methods
Participants.
Twenty-three pairs of monozygotic twins (MZ; 11 male pairs/12 female pairs; age = 25.1 ± 1.5 years, mean ± SD) and 23 pairs of dizygotic twins (DZ; all same-sex pairs; 10 male pairs/13 female pairs; age = 23.5 ± 2.1 years, mean ± SD) were recruited from different families and received high-resolution brain magnetic resonance imaging (MRI) scans and neurocognitive evaluations as part of a 5-year research project evaluating healthy Australian twins and their nontwin siblings, with a projected sample size of ∼1150 at completion (for an overview, see de Zubicaray et al., 2008). Zygosity was established objectively by typing nine independent DNA microsatellite polymorphisms (polymorphism information content >0.7), using standard PCR methods and genotyping. These results were cross-checked with blood group (ABO, MNS, and Rh), and phenotypic data (hair, skin, and eye color), giving an overall probability of correct zygosity assignment >99.99%. All twins were screened to exclude cases of pathology known to affect brain structure. None of the twins reported a history of significant head injury, a neurological or psychiatric illness, substance abuse or dependence, or had a first-degree relative with a psychiatric disorder.
Psychometric intelligence testing.
General intellectual ability was assessed at age 16 (years) (Luciano et al., 2003) using the Multidimensional Aptitude Battery (MAB) (Jackson, 1984), a measure highly correlated with the Wechsler Adult Intelligence Scale, which is designed for assessment of both adults and adolescents aged 16 and older. In this study, we examined three verbal (information, arithmetic, and vocabulary) and two performance (spatial and object assembly) subtests. Each subtest gave a raw score, and verbal (VIQ), performance (PIQ), and full-scale (FIQ) intelligence quotient standardized scores were derived from these sub-tests. The IQ data of one female DZ twin was unavailable due to computer hardware failure, so we excluded her co-twin on subsequent analyses related to IQ. IQ scores for MZ and DZ twins were not significantly different, as previously shown (Luciano et al., 2003). Demographic and IQ data for all subjects, and the correlation coefficients between different IQ scales, are summarized in Table 1 and 2, respectively.
Table 1.
Demographic and IQ data
| MZ | DZ | Significance | |
|---|---|---|---|
| Gender (M/F) | 22/24 | 20/26 | 1.00a |
| Age, years | 25.1 ± 1.5 | 23.5 ± 2.1 | 0.004b |
| Verbal IQ | 110.9 ± 10.9 | 109.8 ± 11.3 | 0.69c |
| Information | 20.9 ± 4.8 | 21.3 ± 6.0 | 0.79c |
| Arithmetic | 12.9 ± 3.0 | 12.0 ± 2.7 | 0.18c |
| Vocabulary | 16.8 ± 4.7 | 17.4 ± 4.6 | 0.64c |
| Performance IQ | 111.2 ± 19.5 | 109.7 ± 15.1 | 0.76c |
| Spatial | 30.3 ± 11.4 | 29.2 ± 9.3 | 0.69c |
| Object assembly | 12.7 ± 4.0 | 12.7 ± 3.2 | 1.00c |
| Full-scale IQ | 111.9 ± 14.8 | 110.5 ± 12.4 | 0.71c |
Values are displayed as mean ± SD. The significance of the difference in proportions, or means, was computed using the aχ2 test,
bindependent t test, or
cone-way repeated measures ANOVA. As the DZ twins were on average a year and a half younger, we detrended the effect of age in our analyses. Other demographic and cognitive measures were for MZ and DZ twins. M, Male; F, female.
Table 2.
Phenotypic correlations between IQ scores
| FIQ | VIQ | INF | ARI | VOC | PIQ | SPA | OBJ | |
|---|---|---|---|---|---|---|---|---|
| FIQ | ||||||||
| VIQ | 0.87 | |||||||
| INF | 0.80 | 0.88 | ||||||
| ARI | 0.68 | 0.80 | 0.51 | |||||
| VOC | 0.55 | 0.64 | 0.66 | 0.16 | ||||
| PIQ | 0.93 | 0.63 | 0.60 | 0.49 | 0.39 | |||
| SPA | 0.87 | 0.59 | 0.59 | 0.47 | 0.31 | 0.93 | ||
| OBJ | 0.78 | 0.52 | 0.47 | 0.36 | 0.43 | 0.85 | 0.60 |
INF, Information; ARI, arithmetic; VOC, vocabulary; SPA, spatial; OBJ, object assembly.
Image acquisition.
All MR images were collected using a 4 Tesla Bruker Medspec scanner (Bruker Medical), with a transverse electromagnetic (TEM) headcoil, at the Center for Magnetic Resonance (University of Queensland, Australia). Three-dimensional T1-weighted anatomical images were acquired with an inversion recovery rapid gradient echo (MP-RAGE) sequence to resolve anatomy at high resolution. Acquisition parameters were: inversion time (TI)/repetition time (TR)/echo time (TE) = 1500/2500/3.83 ms; flip angle = 15°; slice thickness = 0.9 mm with a 256 × 256 × 256 acquisition matrix. Diffusion-weighted scans were acquired using a single-shot echo planar imaging with a twice-refocused spin echo sequence to reduce eddy-current induced distortions (Reese et al., 2003). Acquisition parameters were optimized to provide the best signal-to-noise ratio for estimation of diffusion tensors (Jones et al., 1999). Imaging parameters were: 21 axial slices (5 mm thick), FOV = 23 cm, TR/TE 6090/91.7 ms, 0.5 mm gap, with a 128 × 100 acquisition matrix. 30 images were acquired: 3 with no diffusion sensitization (b = 0, i.e., T2-weighted images) and 27 diffusion-weighted images (b = 1132 s/mm2) in which the gradient directions were evenly distributed on the sphere (Jones et al., 1999). The reconstruction matrix was 128 × 128, yielding a 1.8 × 1.8 mm2 in-plane resolution. The total scan time was 3.05 min.
Registration of structural and diffusion tensor images to a common space.
Before diffusion images may be compared across subjects, all images must be aligned to a common stereotaxic space. For each subject, diffusion tensor (DT) images (denoted by Dij, 1≤ i, j ≤3) were computed from the diffusion-weighted images using the MedINRIA software package (available at http://www-sop.inria.fr/asclepios/software/MedINRIA). Figure 1 explains how the diffusion tensors were estimated from the raw diffusion-weighted scans. One diagonal component image (D11) was manually stripped of nonbrain tissues, yielding a binary brain extraction mask (cerebellum included). The registration process was as follows: (1) Each structural T1-weighted MRI was first aligned to a standardized template defined in the International Consortium for Brain Mapping space (ICBM) (Mazziotta et al., 2001) with a 12 parameter linear transformation using FLIRT (FMRIB's Linear Image Registration Tool) (Jenkinson and Smith, 2001). The ICBM template is one of several standardized adult brain templates and was generated by nonlinearly registering and averaging 27 high-resolution brain MRI scans from the same person in the ICBM standard space to improve the signal-to-noise ratio (Holmes et al., 1998). (2) The masked D11 image was registered to the affine-aligned T1-weighted MRI derived from part (1) with a 12-parameter linear transformation. By combining the transformations in (1) and (2), a concatenated transformation was computed to align the D11 image to the ICBM brain template and also used to resample the D11 image to isotropic voxel resolution (dimension: 128 × 128 × 93 voxels, resolution: 1.7 × 1.7 × 1.7 mm3). The resulting transformation parameters were used to rotationally reorient the tensor at each voxel (Alexander et al., 2001) and then linearly align the tensor-valued images based on trilinear interpolation of the log-transformed tensors (Arsigny et al., 2005). The necessity of processes involved in this step arises from the fact that the directional information at each point in the diffusion images needs to be reoriented when each subject's data is aligned to a stereotaxic space. (3) Since registration accuracy in DTI may be improved by using the full diffusion tensor information in the cost function that guides the registration, rather than its scalar components (Park et al., 2003), we registered all affine-registered DT images in (2) to a randomly selected subject's DT image (a MZ subject), using an inverse-consistent fluid registration algorithm that minimizes the symmetrized Kullback–Leibler divergence (sKL-divergence) of the two tensor-valued images (Chiang et al., 2008). Intuitively, this treats the local diffusion process in each subject as a three-dimensional (3D) field of probability density functions, and uses a fluid mapping, which is based on a standard measure from information theory to quantify the discrepancy between these probability density functions, to drive the tensor data into anatomical correspondence. Selection of an optimal registration target in DTI studies is still an open question. Mori et al. (2008) generated the first population-averaged DTI atlas based on 81 normal subjects linearly aligned to the ICBM space. Since features in a single subject's DTI are more similar to those in other individual DT images than those in a multi-subject atlas, we chose a single subject's DTI scan as the target, which may provide for enhanced registration accuracy (Christensen et al., 2006; Smith et al., 2006; Chiang et al., 2007).
Figure 1.

a, In DTI, a set of diffusion-sensitized images is acquired, with diffusion-sensitizing magnetic field gradients of the same strength, but oriented in different directions on an imaginary sphere. Each voxel in DTI contains multidimensional data (in our study, the dimension is 27). For example, b shows the raw diffusion data from a single voxel (the pink point in a) in all diffusion-weighted images from one of the subjects. Water diffusion is antipodally symmetric along a specific direction, so one diffusion-sensitized image gives a pair of data points with identical values on the sphere. Each point on the sphere indicates the MR signal attenuation caused by water diffusion in the direction of the corresponding diffusion gradient, with greater signal attenuation (color-coded as red; magnitude of MR signal attenuation increases from yellow to red) indicating more rapid rates of water diffusion along that gradient direction. Water diffusion can be estimated by fitting the raw diffusion data in b to a diffusion ellipsoid (c), whose axes correspond to the eigenvalue-eigenvector pairs of a diffusion tensor (Basser and Pierpaoli, 1996). An image of the diffusion tensors estimated from all the voxels of the raw diffusion data is displayed in d (see Fig. 2 for details). Analysis of DTI scans is computationally expensive due to their high information content, especially for the covariance structure analysis in twin studies, so it is more practical to first estimate anisotropy maps of scalar values, such as FA (e).
For region-of-interest (ROI) analyses, masks of cerebral lobes, defined on the ICBM brain template according to a standardized anatomical protocol (https://cms.loni.ucla.edu/NCRR/protocols.aspx), were mapped to the DT images by nonlinearly registering the ICBM template to subjects' T1-weighted MRI and were then transferred from the T1-weighted MRI to the DT image using the affine transformation above. The nonlinear registration was based on maximizing the Jensen–Rényi divergence (JRD) of the joint intensity histogram, using a fully 3D fluid transformation which deforms the image according to the laws of continuum mechanics (Chiang et al., 2007). All computational processes were executed using a 306-node, dual-processor SUN Microsystems V20z cluster. Each compute node has a dual 64-bit 2.4 GHz AMD Opteron CPU. The registration processes were performed in parallel by submitting one subject's process to one compute node, and the average computation time was ∼5.5 h by a single processor.
Definition of regions with high fractional anisotropy.
A fractional anisotropy (FA) map was constructed from each fluidly registered DT image. FA is defined as the ratio of the SD to the root mean square of the eigenvalues of a diffusion tensor (Basser and Pierpaoli, 1996). Higher FA values indicate that water diffusion is more anisotropic, or more constrained by the ordered arrangement of myelinated fibers in the white matter (Beaulieu, 2002). This is visualized in Figure 2, where the shape of tensor ellipsoids is more prolate in regions with higher FA, such as the genu of the corpus callosum. FA also tends to be higher in regions that are more heavily myelinated, and in regions where there is a dominant fiber direction that constrains the directional profile of water diffusion. We averaged the FA images across all 92 subjects and restricted subsequent data analysis to regions in which the average FA >0.3, as in Smith et al. (2006). This may sacrifice some of the information that DTI can provide. However, given the sample size in this pilot study (N = 92), we preferred to focus our regions of interest on major white matter fiber structures (Smith et al., 2006), as more highly anisotropic regions may have a better signal-to-noise ratio for measures derived from the diffusion images, and less residual misregistration error as a result of intersubject morphological variations. To reduce noise and improve the sensitivity of group comparisons (Leung et al., 2004; Smith et al., 2006), the FA map of each subject was smoothed using an isotropic Gaussian filter (FWHM = 12 mm).
Figure 2.
The image of diffusion tensors (a) selected from the brain region at the junction of the corpus callosum and the corona radiata, shown as the yellow box in the corresponding FA image (b) of the same subject as in Figure 1. Diffusion tensors are visualized as ellipsoids (which have been normalized to unit mass) that are color coded, as is conventional, to represent the orientation of the normalized principal eigenvector (dominant direction of water diffusion) relative to the medial–lateral axis (coded in red), anterior–posterior axis (coded in green), and superior–inferior axis (coded in blue) of the anatomical reference frame. Glyphs of tensor ellipsoids were generated using the visualization software “BrainSuite” (http://www.loni.ucla.edu/Software/) (Shattuck et al., 2008).
Univariate structural equation modeling.
To estimate genetic and environmental twin correlations, and the relative contributions of additive genetic (A), shared environmental (C), and unshared or unique environmental (E) components to the observed variable, y, we used structural equation models (Fig. 3a) (SEM) (Neale et al., 1992; Schmitt et al., 2007). Shared (i.e., common) environment refers to aspects of the family rearing environment and other experiences shared by both siblings in a twin pair, while unshared environment refers to the unique experiences that each twin does not share with their co-twin. For each twin, we modeled the voxel value of FA as the sum of several latent factors, y = aA + cC + eE, where the variance of A, C, and E, respectively var(A) = a2, var(C) = c2, and var(E) = e2, denotes their relative contribution to the variance of the observed variable, y, given that var(y) = a2+ c2+ e2. The covariance of trait y between the first and second twin in the same pair is a2+ c2 for MZ twins, and (1/2)a 2+ c2 for DZ twins, because, on average, MZ twins share all and DZ twins share half of their genetic polymorphisms (these are random variations in the DNA sequence that occur even across normal individuals). Since A, C, and E are unobservable variables, the path coefficients θ = (a, c, e) were estimated by comparing the variance-covariance matrix derived from the model above, and the sample covariance matrix from the observed values of y, using maximum-likelihood fitting (Fornell and Larcker, 1981). Minus two times the log-likelihood ratio, written as TML,θ, follows a χ2 distribution with p(p + 1) − t degrees of freedom, where p = 2 is the number of observed variables, and t = 3 is the number of free model parameters. TML,θ was estimated using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method (Press et al., 2002). Acceptance of the null hypothesis (p > 0.05) indicates a good fit for the model.
Figure 3.
Path diagrams for (a) univariate (for FA) and (b) bivariate cross-trait (for FA and IQ) structural equation models (a and b are adapted from Neale et al., (1992) and Miles et al., (2002) respectively. a, Each twin's phenotypic measure (e.g., FA in this study) is assumed to be determined by additive genetic (A) and environment factors. Environmental factors are further subdivided into those that the co-twins share (denoted by C, e.g., family rearing environment, and common developmental factors in utero), and those that are unique for each twin (denoted by E, e.g., they may be educated at different schools). Contributions of the ACE factors to the phenotype are indicated by single arrows and assumed to be the same between co-twins (twin 1 and twin 2) for simplification, with their weights, or path coefficients, denoted by a, c, and e, respectively. Random noise, or experimental measurement error, is included in component E, and assumed to be independent between twin 1 and 2 (no correlation). Correlations in the genetic and shared environmental factors between co-twins are indicated by double arrows. For A1 and A2, the correlation coefficient is equal to 1 for MZ and 0.5 for DZ twin pairs. The correlation coefficient between C1 and C2 is always 1 from the definition of the shared environment. b, In bivariate cross-trait SEM, we assume that there are common genetic and environmental factors that affect various phenotypes within an individual. Here, we only consider factors that affect two phenotypes, such as FA and IQ. The effects of these common factors are estimated by comparing the difference between MZ and DZ pairs, in the correlation between the two phenotypes within the same individual (cross-trait within-individual), and also in the correlation between one phenotype in one twin, and the other phenotype in the other twin (cross-trait cross-twin). The cross-trait within-individual correlation (the correlation between FA and IQ in twin 1 or in twin 2, shown as connected by gray arrows) is divided into additive genetic, and shared and unique environmental components (e.g., AFA, i, CFA, i, and EFA, i for FA, and AIQ, i, CIQ, i, and EIQ, i for IQ; i = 1 or 2 for twin 1 or 2), and the correlation coefficients between AFA, i and AIQ, i, CFA, i and CIQ, i, and EFA, i and EIQ, i, are denoted by ra, rc, and re, respectively. The cross-trait cross-twin correlation is shown as AFA, i and AIQ, j, and CFA, i and CIQ, j connected by black arrows, for FA in twin i and IQ in twin j, where i, j = 1 or 2, and i ≠ j. There is no re term for EFA, i and EIQ, j, because the unique environmental factors between subjects are not correlated. The covariance across the two phenotypes within the same subject, or separately in the two subjects, is then derived by multiplication of the path coefficients for the closed paths in the path diagram. For example, covariance between FA in twin 1 and IQ in twin 2 is equal to aFA·ra·aIQ+cFA·rc·cIQ for MZ twins, and aFA·1/2ra·aIQ+cFA·rc·cIQ for DZ twins. This implies that any excess in cross-trait cross-twin correlation in MZ twins over that in DZ twins is attributed to common genetic factors that affect both FA and IQ. Correlations for the same phenotype (FA or IQ) between co-twins, as have already been described in a, are not shown for simplification.
We fitted the structural equation model to the covariance of FA at each voxel to estimate at each voxel the relative contributions of genetic and environmental factors to variance in white matter integrity measures in the white matter. Since the MZ twins were slightly but significantly older than the DZ twins, the voxel FA value was adjusted for age and sex before model fitting (for the univariate analysis here and also the cross-trait analysis below) (McGue and Bouchard, 1984), to avoid inflation of the between-pair correlations and thus the estimated effects of shared environment due to possible associations between FA and age or sex. We also applied Levene's test to each voxel (Brown and Forsythe, 1974) to test the assumption of homogeneity in variances across the MZ and DZ twins, and found that there was no significant difference in variances between the two types of twins (FDR = 1.0; see below for details of FDR). It is standard in twin studies to examine whether the observed measures are best modeled using a combination of additive genetic, shared, and unshared environmental factors, or whether only one or two of these factors is sufficient to explain the observed pattern of inter-twin correlations. We started from the full model involving all 3 variance components, ACE: θ = (a, c, e), and compared it with the more restricted models, AE: θ = (a, e) and CE: θ = (c, e). Under the rule of parsimony, AE or CE were considered to fit the data better than ACE if their model-fitting p value was >0.05 (note that this differs from the more standard usage for p values in which values >0.05 are disregarded). In this case, we selected AE or CE depending on which one had the smaller χ2 value, and the selected AE or CE model was further compared with E:θ = (e) to determine the best model. The significance of the genetic (p(A)) and the shared environmental (p(C)) factors was determined by the difference between the log-likelihood of the full (ACE) and the restricted (CE) model for p(A), and was determined by the difference between the log-likelihood of the full (ACE) and the restricted (AE) model for p(C). The log-likelihood for the full and the restricted models were denoted by log(Lf) and log(Lr) respectively. Minus two times this difference, or −2{log(Lr) − log(Lf)}, is asymptotically distributed approximately as a χ2 distribution with one degree of freedom.
Linking diffusion anisotropy with intellectual performance.
We used random-effects regression models (RRM) (Hedeker et al., 1994) to measure correlations between FA and IQ scores (including the sub-test scores). Ordinary regression methods are inappropriate here because observations are correlated within twin pairs, violating the assumption that observations must be statistically independent. In RRM, this dependency is addressed by adding a random variable αi, to incorporate the clustering of the observed variables within the ith pair, into the ordinary regression equations: yi = Xi β + 1i αi + εi.
Here, yi = the 2 × 1 vector of observed variables (FA) within the ith pair, β = a (q+1) × 1 vector of unknown regression coefficients, Xi = a known 2 × (q + 1) covariate matrix, 1i = a 2 × 1 vector of ones, and εi represents the 2 × 1 error vector. q was set to 3, with the subjects' IQ score, age, and sex as the covariates. We estimated these unknown parameters (β and αi) based on maximum marginal likelihood (MML) methods detailed in (Hedeker et al., 1994). The significance of the correlation between FA and IQ was determined by comparing the full (IQ, age, and sex) and the restricted (age and sex only) models, as described above.
Cross-trait cross-twin analysis of FA and intelligence.
For IQ scores that were significantly correlated with FA (with FDR <0.05), we performed a “cross-trait cross-twin” analysis to detect common genetic or environmental factors influencing both fiber architecture and intelligence. Cross-trait cross-twin analyses estimate the genetic and environmental contributions to the correlations between two phenotypes (FA and IQ in this study) in the same set of subjects (Posthuma et al., 2002; Hulshoff Pol et al., 2006). The path diagram is shown in Figure 3b. If the correlation between the voxel value of FA in one twin and the level of IQ in the other twin (“cross-trait” and “cross-twin”) is greater in MZ pairs than in DZ pairs, the excess in the MZ correlation over the DZ correlation is then assumed to be attributable to common genetic factors that mediate both white matter integrity and intelligence. Formally, we modeled the genetic and environmental contributions to FA and intellectual performance for subject j (j = 1 or 2) by defining xj = axAxj + cxCxj + exExj, and yj = ayAyj + cyCy j+ eyEyj, where x stands for the voxel value of FA, y for IQ, and A, C, and E respectively denote the additive genetic, shared and unshared environmental components. Cross-trait correlations between FA and intellectual performance were then derived from the covariance matrix of vector w = (x1, x2, y1, y2)T, where T denotes transpose, given by the following:
 |
where Φxx and Φyy are the covariance matrices for phenotype x or y between subject 1 and 2, as was described in the univariate SEM above. Φxy is the cross-trait covariance matrix, composed of the covariance between the two traits within the same individual (cov(x1, y1) and cov(x2, y2)), and the cross-trait cross-twin covariance (cov(x1, y2) and cov(x2, y1)), as detailed below:
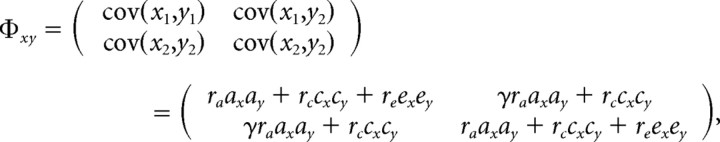 |
where γ = 1 for MZ twins, and 1/2 for DZ twins. ra, rc, and re are the cross-trait correlation coefficients for Ax and Ay, Cx and Cy, and Ex and Ey. A higher value of ra indicates that the two phenotypes are more likely mediated by a common set of genes (Lange and Boehnke, 1983; Seeman et al., 1996). The path coefficients were estimated by comparing the covariance matrix implied by the model and the sample covariance matrix of the observed variables, using maximum-likelihood fitting to give a χ2 value. We started from the full set of path coefficients (ax, cx, ex, ay, cy, ey, ra, rc, re) and removed one of ax, cx, ay, and cy from the model step by step. Removing ax or ay/cx or cy also removed ra/rc. e1, e2 and re were always kept in the model to include random noise. Selection of submodels was determined by the rule of parsimony, i.e., a model was considered “better” if the difference in χ2 values between it and the more comprehensive model at the previous step was not significant. If two models contained the same number of parameters, the model with a smaller χ2 value was considered better. Model selection ended when the best model was achieved, i.e., when either (1) all possible more restricted models were not better than the current model or (2) the current model contained e1, e2 and re only. If ra or rc was included in the best model, the significance of ra or rc was then determined by comparing the χ2 values of the best model and its submodel where ra (or rc) = 0. The cross-trait model fitting was performed only at voxels where the FDR-adjusted p value (see below) of the correlation between FA and IQ was <0.05.
Correction for multiple comparisons.
All statistical maps in this study were further assessed using the false discovery rate method (FDR) (Benjamini and Hochberg, 2000; Storey and Tibshirani, 2003) to correct for multiple comparisons. FDR is defined as the expected proportion of false positive findings out of all rejected tests. For example, FDR = 0.05 means that 5% of the voxels that are identified to be significant are in fact false positive findings. Here, we consider the test statistic at a given voxel to be significant when its p value is not greater than a primary threshold γ set to 0.01. The 5% is an estimate that will be true on average when the method is used, as the FDR method controls the expected false discovery rate, or the expected proportion of false positives in the map. In other words, it is expected that, on average using this method, 95% of the voxels labeled as significant will be true positive findings. Mathematically, FDR(γ) ≈ m0·γ/S(γ), where S(γ) is the number of voxels labeled as significant. m0 is the total number of voxels where the null hypothesis is true, which is unknown and has to be estimated from the empirical distribution of the voxel p values (Storey and Tibshirani, 2003). γ is the rejection rate for the null hypotheses, so m0·γ equals the number of false positive voxels. As is conventional in brain mapping studies, statistical maps with an FDR value <0.05 were considered to reach overall significance. To visualize brain regions where the test statistic is significant after correction for multiple comparisons, we constructed maps of FDR-adjusted p values, so that if we consider voxels with the adjusted p value < α to be significant, then the FDR across the statistical map will be less than α (α was set to 0.05 by convention). FDR-adjusted p values can be estimated as follows: Let p(1) ≤ p(2) ≤ … ≤ p(m) be the rank-ordered p values of all m voxels, then the FDR-adjusted p value for voxel m is given by p̃ (m) = FDR(p(m)), and p̃(i) = min(p̃(i+1), FDR(p(m))), for voxels i = m − 1, …, 1, sorted in descending order (Storey and Tibshirani, 2003).
Results
Maps of genetic influences on white matter integrity (FA)
Figure 4 reveals the profile of genetic versus environmental influences on white matter integrity (as quantified by FA). The first column shows the significance of the genetic effect, while the remaining 3 columns show the proportion of the variance in the 92 twins attributable to genetic, common and unique environmental factors. Clearly, white matter integrity is under significant genetic control in all posterior white matter regions (Fig. 4, first column), with high heritability values (a2). The heritability of white matter integrity may be regarded as the proportion of the observed variation in FA values that may be attributed to genetic differences among individuals. Genetic factors explained between 75 and 90% of the observed variance in white matter integrity in almost all white matter regions (Fig. 4, second column).
Figure 4.
Maps of genetic influences on white matter integrity. These maps show how different factors, genetic or environmental, explain different proportions of the observed variance in white matter integrity across 92 subjects. The Montreal Neurological Institute (MNI) coordinate (which is also the coordinate used in the ICBM space; expressed in mm) of the slices is indicated at the beginning of each row. The first column shows the statistical significance of the genetic influences (p(A), FDR-adjusted), and the proportional contributions to the overall variance in FA, from genetic (a2), shared environmental (c2) and unique environmental (e2) factors (the second to the last columns, computed under the best-fitting statistical model). The genetic effect is detected in the genu and the splenium of the corpus callosum (x = 0), the right cerebral peduncle, and right ILF/IFO (z = −14), the anterior limbs of the internal capsule bilaterally, and the left posterior thalamic radiation/optic radiation (z = 5), the superior longitudinal fasciculus bilaterally (z = 22), and the superior and posterior corona radiata bilaterally (z = 35). A, Anterior; R, right.
White matter integrity, as measured by FA, was under strong genetic control in the genu and the splenium and part of body of the corpus callosum, the right cerebral peduncle, and right inferior longitudinal fasciculus (ILF)/inferior fronto-occipital fasciculus (IFO), the anterior limbs of the internal capsule bilaterally (which contain the corticobulbar tract and superior thalamic radiations). Other regions with strong genetic control of white matter integrity included the left posterior thalamic radiation/optic radiation, the superior longitudinal fasciculus bilaterally, and the superior and posterior corona radiata (FDR for p(A) = 0.01 over the whole brain, including only voxels with FA >0.3). The voxel-level maps p(A) were significant only in regions with extremely high heritability values near 100% (this can be seen by comparing columns 2 and 1 of Fig. 4, which show heritability values throughout the white matter, and their significance). Contributions from shared environmental factors were not detectable (FDR for p(C) = 1.00).
Genetic influences in lobar subregions
Because the pattern of genetic versus environmental influences may differ in different lobes of the brain, we also fitted genetic models to the regional average values of FA in regions of interest defined by the ICBM atlas. As shown in Table 3 and Figure 5, the average FA in white matter (defined as the region with group mean FA >0.3) served as the observed variable for the ACE structural equation models. The highest heritability values were observed in the parietal lobes bilaterally, with a2 reaching 84.8% on the left and 84.3% on the right. Parietal fiber integrity is therefore under strong genetic control. When voxel FA data summarized in lobar regions were fitted for the full ACE model, the shared environmental effects were detected but not significant at the left temporal lobe and the right occipital lobe, and the effects of unique environment were relatively small, except for the right occipital lobe where additive genetic, shared environmental, and unique environmental effects were approximately equal. Only the genetic and the unique environmental effects were detected in the best-fitting model. The genetic influence was found to be significant in bilateral parietal lobes (both with p(A) < 0.001), bilateral frontal lobes (p(A) = 0.04, for the left frontal lobe; p(A) = 0.006, for the right frontal lobe), and for the left occipital (p(A) = 0.003) lobe (Table 3).
Table 3.
Twin correlations and variance components estimated from the values of the lobar FA
| Twin correlations |
Percentage of variance estimated under the best model |
Percentage of variance estimated under the full model |
p(A) | p(C) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MZ | DZ | a2 | c2 | e2 | a2 | c2 | e2 | |||
| Frontal-L | 0.45* (0.07, 0.72) | 0.01 (0, 0.28) | 55.0 (15.3, 100.0) | − | 45.0 (24.7, 85.2) | 55.0 (4.6, 100.0) | 0.0 (0, 32.2) | 45.0 (24.7, 85.2) | 0.04 | 1.0 |
| Frontal-R | 0.65* (0.34, 0.83) | 0.05 (0, 0.43) | 73.5 (37.0, 100.0) | − | 26.5 (14.7, 53.2) | 73.5 (30.0, 100.0) | 0.0 (0, 31.5) | 26.5 (14.7, 53.2) | 0.006 | 1.0 |
| Parietal-L | 0.79* (0.58, 0.90) | 0.02 (0, 0.41) | 84.8 (52.1, 100.0) | − | 15.2 (8.5, 31.4) | 84.8 (51.1, 100.0) | 0.0 (0, 25.7) | 15.2 (8.5, 31.4) | < 0.001 | 1.0 |
| Parietal-R | 0.80* (0.60, 0.91) | 0.12 (0, 0.49) | 84.3 (53.0, 100.0) | − | 15.7 (8.9, 31.2) | 84.3 (48.2, 100.0) | 0.0 (0, 33.4) | 15.7 (8.9, 31.2) | < 0.001 | 1.0 |
| Temporal-L | 0.74* (0.49, 0.88) | 0.56* (0.21, 0.78) | 83.0 (54.7, 100.0) | − | 17.0 (10.2, 31.1) | 43.9 (0, 100.0) | 38.8 (0, 96.3) | 17.3 (10.1, 33.4) | 0.06 | 0.19 |
| Temporal-R | 0.67* (0.37, 0.84) | 0.19 (0, 0.54) | 65.2 (34.8, 100.0) | − | 34.8 (21.1, 61.4) | 65.2 (0, 100.0) | 0.0 (0, 75.2) | 34.8 (21.1, 62.7) | 0.10 | 1.0 |
| Occipital-L | 0.65* (0.35, 0.83) | 0.03 (0, 0.42) | 75.6 (39.6, 100.0) | − | 24.4 (13.5, 49.4) | 75.6 (35.4, 100.0) | 0.0 (0, 28.8) | 24.4 (13.5, 49.4) | 0.003 | 1.0 |
| Occipital-R | 0.61* (0.28, 0.81) | 0.42* (0.03, 0.70) | 65.0 (35.2, 100.0) | − | 35.0 (21.4, 61.2) | 33.6 (0, 100.0) | 30.1 (0, 95.7) | 36.3 (21.5, 65.1) | 0.36 | 0.44 |
For each lobe, the average FA in white matter (defined as FA > 0.3) served as the observed variable for the ACE structural equation models. Values in parentheses indicate the 95% confidence interval, computed using the likelihood-based method (Neale and Miller, 1997). Statistical significance of the relative contributions to the total variance of the lobar FA by the genetic (A) and the shared environmental (C) factors is denoted by p(A) and p(C), presented in bold font if p(A) or p(C) < 0.05. Twin correlations were computed based on the analysis of variance for clustered measures, by comparing the between-group (each twin pair was treated as an individual group) variation and the total variation in values of the lobar FA (Ukoumunne, 2002).
*p < 0.05. L, Left; R, right.
Figure 5.
Proportions of variance in white matter integrity in different lobes of the brain (average lobar values of FA) due to genetic (a2), shared environment (c2) and unique environment (e2) components, under the full (a) and the best-fitting model (b). For each lobe, the average FA in white matter (defined as FA >0.3) served as the observed variable for the ACE structural equation models. *p(A) = 0.04; **p(A) = 0.006, #p(A) < 0.001; ##p(A) < 0.001; §p(A) = 0.003. p(A) in other lobes and p(C) are not significant. These data show the dominant effect of genes on white matter integrity and provide little evidence to support a strong environmental effect (that is independent of genetic variation). L, Left; R, right.
Mapping phenotypic and genetic correlations between FA and IQ scores
White matter integrity, measured by FA, was significantly correlated with full scale IQ, and also with performance IQ, but not with verbal IQ. Among all IQ scores tested using RRM, with age and sex controlled, the full-scale IQ (FIQ), performance IQ (PIQ) and one of its sub-tests, object assembly (OBJ), were found to correlate significantly with FA (Table 4). Because correlations are plotted voxel by voxel across the brain, the significance of the overall pattern of correlations, adjusted for multiple comparisons, is assessed using the false discovery rate value, with values <0.05 being regarded as significant.
Table 4.
Overall significance of correlations between FA and IQ scores
| FDR valuesa | |
|---|---|
| Verbal IQ | 1.00 |
| Information | 0.67 |
| Arithmetic | 1.00 |
| Vocabulary | 1.00 |
| Performance IQ | 0.01 |
| Spatial | 0.13 |
| Object assembly | 0.007 |
| Full-scale IQ | 0.04 |
FDR < 0.05 (presented in bold font) indicated that 5% of the voxels in which FA was found to be associated with the IQ score are in fact false positive findings. In other words, 95% of the associations labeled are true. The maps of negative correlations between each of these measures and FA were not significant.
aFDR was computed only in regions where the individual IQ score correlated positively with FA.
Figure 6 shows the pattern of correlations between each cognitive measure and white matter integrity. It is clear that there is a pervasive correlation between white matter integrity in almost all regions and intellectual performance. When the correlations are assessed within the corpus callosum at midline, there is a prominent region of correlation (r ∼ 0.3–0.5 locally) between each cognitive score and white matter integrity at the callosal isthmus. Such a correlation might be considered surprisingly high for an image-derived measure, and the commissural fibers carried in the callosal isthmus innervate the parietal cortices, which may be recruited in tasks such as object assembly.
Figure 6.
Association between FA and FIQ, PIQ and OBJ. Partial correlation coefficients are shown between white matter integrity (measured using FA) and the intellectual performance scores: FIQ, PIQ, and OBJ. The MNI coordinate (mm) of the slices is indicated at the beginning of each row. All statistics are controlled for age and sex, and are computed voxelwise for subjects randomly selected, one from each pair (the left column in each group shows the correlation coefficient, and the right column shows its significance). Overall significance is measured by FDR-adjusted p values obtained from the random-effects regression model (RRM), as RRM also estimated the effect of twin pairing. Significant positive correlation between FA and FIQ, PIQ or OBJ was detected in the isthmus of the corpus callosum and the cingulum bundle (x = 3), the bilateral cerebral peduncles (for PIQ and OBJ) and ILF/IFO (for the object assembly test, OBJ) (z = −14), the posterior limbs of the internal capsule bilaterally and left posterior thalamic radiation/optic radiation (z = 3), the anterior corona radiata and right superior fronto-occipital fasciculus (z = 20), and the superior and posterior corona radiata bilaterally (z = 35). Negative correlations were not significant. Regions where FA is associated with OBJ are the most extensive and have the greatest effect sizes.
Specifically, FIQ, PIQ, and OBJ scores were positively correlated with white matter integrity, as measured by FA, in the isthmus of the corpus callosum and the cingulum (r ∼ 0.3–0.4), in the cerebral peduncles bilaterally (for PIQ and OBJ scores), ILF/IFO (for the OBJ score), bilateral posterior limbs of the internal capsule (which contain the corticobulbar and corticospinal tracts and the superior thalamic radiations) and in the left posterior thalamic radiation/optic radiation, right superior fronto-occipital fasciculus, and bilateral anterior, superior and posterior corona radiata (Fig. 6). The effect size for these correlations with white matter integrity was greatest for the object assembly subscale, with highest effect sizes in the parietal lobe. Performance on this task may benefit from increased myelination, which may enhance physiological parameters such as axonal conduction speed and may also be reflected in diffusion-sensitive indices such as FA.
We further subdivided the cross-trait phenotypic correlation between FA and FIQ, PIQ, or OBJ into genetic (ra), and shared (rc) and unique (re) environmental components. As there is a strong genetic influence on fiber architecture throughout the brain, perhaps most prominently in the parietal lobes, and given the correlation between IQ scores and white matter integrity in the same region, it is plausible that overlapping sets of genes may influence IQ measures and fiber architecture. One common way to determine whether partially overlapping genes affect two different traits (here FA and IQ) is to use a measure of one trait in one twin to predict the level of the other trait in the other twin. If such a prediction can be made with greater precision in identical than fraternal twins, then a common set of genes must be involved.
Figure 7 shows these cross-trait maps, which suggest that the IQ of one twin may be predicted, with a high degree of precision, from the white matter integrity of the other twin. An overlapping set of genes therefore mediates this correlation. FA and FIQ, PIQ or OBJ scores were influenced by an overlapping set of genes in the cingulum and isthmus of the corpus callosum, the cerebral peduncles and ILF/IFO (for OBJ), the posterior limbs of the internal capsule and the left posterior thalamic radiation/optic radiation (for PIQ and OBJ), the right superior fronto-occipital fasciculus, and the anterior, superior and posterior (for PIQ and OBJ) corona radiata bilaterally (Fig. 7) (FDR for p(ra > 0) = 0.015 for FIQ, 0.027 for PIQ, and 0.016 for OBJ; negative ra was not significant). We did not find any significant effects for shared environmental factors between intellectual performance and white matter integrity (rc).
Figure 7.
Cross-trait genetic correlations between FA and FIQ, PIQ and OBJ scores, with maps of correlation coefficients ra, corrected for age and sex (left), and the FDR-adjusted values for the significance of ra (right). The MNI coordinate (mm) of the slices is indicated at the beginning of each row. For each of these IQ scores, cross-trait analysis was limited to the brain regions where phenotypic correlation between FA and that IQ score was significant. Common genetic factors affect both FA and FIQ, PIQ or OBJ in the cingulum and isthmus of the corpus callosum, a commissural pathway innervating the parietal cortex, which is crucial for multi-modal sensory integration (x = 3), the cerebral peduncles (for OBJ) and ILF/IFO (right > left, for OBJ) (z = −14), the posterior limbs of the internal capsule and the left posterior thalamic radiation/optic radiation (for PIQ and OBJ) (z = 3), bilateral anterior corona radiata and right superior fronto-occipital fasciculus (z = 20), and bilateral superior and posterior corona radiata (for PIQ and OBJ) (z = 35). There were no negative genetic correlations between IQ scores and white matter integrity, i.e., negative values of ra were not significant.
Comparisons of registration accuracy between MZ and DZ twins
It is certainly possible in theory that the overall accuracy of cross-subject anatomical registration is better in the group of MZ twins than in the group of DZ twins. Even so, the smaller intra-pair morphological variations in the MZ twins does not imply that the cross-subject variance is less within the group of MZ twins as a whole; in fact, they are likely to be as variable in anatomy across subjects as randomly picked pairs of unrelated individuals, of the same age and sex. It is worth noting that the twins' images are not registered by aligning one twin's image directly to the other twin's image; instead, they are each individually aligned to a common target image from a randomly selected control subject who is not a member of the twin pair. As such, because the MZ twins vary as much, as a group, as the DZ group (and the general population), what matters most for registration is how much they deviate from the target image. As the target image was not the other member of the pair (except for the co-twin of the subject who served as the target), but an unrelated individual, a zygosity × registration error interaction is unlikely. Even so, there remains the empirical possibility that registration errors to the common target image were not the same for each twin group. To test whether this was the case in our subjects, we compared the registration accuracy for the groups of MZ twins versus the group of DZ twins using three overlap measures: Total overlap:
 |
Mean overlap:
 |
Union overlap:
 |
where Sr is the mask derived from regions where FA >0.3 in the source DTI and then warped by the fluid deformation fields that registered the source DTI to the target DTI, and Tr is the mask derived from regions where FA >0.3 in the target DTI. |.| indicates the volume computed as the number of voxels. The measures of overlap can be used to determine how well anatomy is aligned to the common template across a group of subjects. Importantly, there were no statistically significant differences between the MZ group and DZ group for any of the overlap measures (Mean ± SD, MZ twins vs DZ twins: 0.527 ± 0.059 vs 0.512 ± 0.047 for TO, 0.499 ± 0.046 vs 0.495 ± 0.042 for MO, 0.334 ± 0.038 vs 0.329 ± 0.035 for UO). As such, we do not expect the higher FA affinity among MZ pairs to be attributable to systematic differences in cross-subject registration accuracy, at the group level, between the two types of twins.
Discussion
This study had three main findings. First, white matter integrity was under strong genetic control; genetic factors explained almost 80% of the variance, with highest heritability in parietal brain regions. Second, white matter integrity was linked with intellectual performance, with correlations as high as 0.3–0.4 between performance IQ and white matter integrity. Third, using a cross-trait mapping approach, we implicated the same genes as mediating the correlation between IQ and white matter integrity, suggesting a common physiological mechanism for both.
Fiber architecture in most major white matter structures was highly heritable, consistent with prior MRI-based reports that brain morphometry is also highly heritable (Toga and Thompson, 2005). Over 50% of the variation in white matter integrity was due to genetic influences in the genu and the splenium of the corpus callosum, cerebral peduncles, right inferior longitudinal fasciculus/inferior fronto-occipital fasciculus, anterior limbs of the internal capsule/corticobular tract/superior thalamic radiation, left posterior thalamic radiation/optic radiation, the superior longitudinal fasciculus, and the corona radiata.
Our finding that FA is highly heritable in the genu and splenium of the corpus callosum is consistent with the only other study using diffusion imaging in twins. Pfefferbaum et al. (2001) found that genetic contributions explained 67% and 49% of the total variance in FA in the splenium and genu, respectively. In our study, variance in FA was heavily influenced by genetic factors (a2 constituted ∼50–80% of total variation). FA may reflect underlying levels of axonal myelination, which may account for differences in reaction times, processing speed, and intellectual performance across subjects. As noted by Neale et al. (1992) and many others, a genetic effect on brain architecture does not imply that environmental factors are unimportant for development; in many cases beneficial genes and environmental factors are highly correlated; talented individuals, for example, may tend to seek out activities and environments that in turn promote improved brain function (see Gray and Thompson, 2004, for a discussion of gene × environment interactions, and IQ). Moreover, shared environmental influences on FA may not be totally excluded, because the classical twin design may slightly overestimate heritability by attributing the excess in the MZ pair correlation over the DZ pair correlation only to genetic effects (Grayson, 1989; Hopper and Visscher, 2005).
Imaging measures, such as FA, that are heritable and link with cognition may empower the search for specific genetic polymorphisms (quantitative trait loci) that impact white matter structure. A specific variant of the Neuregulin 1 (NRG1) gene has been associated with reduced white matter density and anisotropy (McIntosh et al., 2008), and in another study, hypomyelination in the hippocampus and optic nerves was observed when the Bace1 gene was knocked out (Hu et al., 2006). The association between diffusion imaging measures and IQ may stem from the fact that both are sensitive to underlying levels of myelination, with common set of genes influencing them both.
Higher FA was linked with higher FIQ, PIQ or OBJ in the isthmus of the corpus callosum, the cingulum, cerebral peduncles, ILF/IFO, posterior limbs of the internal capsule bilaterally, left posterior thalamic radiation/optic radiation, right SFO, and the anterior, superior and posterior corona radiata bilaterally. The correlation coefficient was around 0.3–0.4 in most regions, close to the correlation coefficient observed between FIQ/PIQ and frontal gray matter volumes (Thompson et al., 2001), white matter density (Hulshoff Pol et al., 2006), and white matter FA (Schmithorst et al., 2005). Correlations between FA and FIQ, PIQ or OBJ in most of these regions were mediated by common genetic factors. The fiber systems whose integrity was most tightly linked with IQ include several with critical roles in visuospatial processing. The callosal isthmus interconnects bilateral primary visual and visual association areas of the parietal and occipital cortex, and is involved in visuospatial memory (Begré et al., 2007). The cingulate gyrus, and the cingulum bundle that runs within it, integrate information regarding motivation, error evaluation, and emotion, and modulate cognitive, motor, endocrine and visceral responses (Bush et al., 2000). Gray matter density in the anterior cingulate is associated with FIQ (Wilke et al., 2003; Frangou et al., 2004; Haier et al., 2004), whereas the mean diffusivity in the posterior cingulate is correlated with cognitive ability in patients with Alzheimer's disease (Yoshiura et al., 2002). The superior and inferior fronto-occipital fasciculus, tracts whose integrity is highly heritable, are part of a widely distributed visuospatial attention network. The superior fronto-occipital fasciculus innervates the dorsolateral prefrontal cortex, while the inferior fronto-occipital fasciculus innervates the ventrolateral prefrontal and medial orbitofrontal cortex (Wakana et al., 2004; Makris et al., 2007). Disconnection of inferior fronto-occipital fasciculus can cause visual neglect (Urbanski et al., 2008).
Our findings are consistent with morphometric data by Luders et al. (2007, 2008), who found that the midsagittal thickness at the isthmus of the corpus callosum was positively correlated with FIQ, PIQ, and VIQ, with greatest effect sizes for FIQ and PIQ. Hines et al. (1992) also observed that the midsagittal surface area of the genu and isthmus of the corpus callosum positively correlated with visuospatial ability. Moreover, Yu et al. (2008) found that higher values of FA in the optic radiation and pyramidal tract, were associated with higher PIQ. Our results also build upon the voxel-based morphometry study by Hulshoff Pol et al. (2006), in which the white matter density, a measure derived from structural MRI, in the superior fronto-occipital fasciculus, corpus callosum, and left optic radiation was correlated with PIQ; such correlations were attributable more to genetic influences than to environmental factors. However, we failed to find any significant correlation between our white matter measures and verbal IQ. It may be that performance IQ, rather than verbal IQ, is more tightly associated with physiological parameters such as nerve conduction velocity, which may be linked with diffusion anisotropy, and is sensitive to the level of axonal myelination (Arbuthnott et al., 1980; Beaulieu, 2002; Tyszka et al., 2006). In future, we will explore associations between white matter integrity and other cognitive measures, specifically processing speed, in a larger sample.
Certain disorders provide exceptions to the theory that high fiber anisotropy correlates with high IQ. Individuals with Williams Syndrome, which is characterized by impaired visuospatial ability but relatively intact language production, have profoundly lower PIQ than typically developing subjects, but FA in their bilateral superior and inferior longitudinal fasciculus, and right superior fronto-occipital fasciculus was significantly higher (Hoeft et al., 2007). The authors attributed this to increased myelination and abnormal myelin packing in Williams syndrome. Consequently, there may be a complex relationship between fiber architecture and intelligence.
Several issues remain in our study. First, although the brain architecture of identical twins is more similar than the brain architecture of fraternal twins, we found, using overlap measures, that the overall registration accuracy was not statistically better in identical than in fraternal twins. This is because the registration accuracy to a common template depends more on the group variance than the intra-pair differences, as all twins are registered to a target image of an individual who is not related to them (except for the co-twin of the subject who served as the target). Even so, further empirical studies of zygosity × registration error interactions are of interest in heritability studies, because when they are significant, they could lead to inflated estimates of heritability. Second, the age range of our subjects is narrow and as such we could not model the influence of age on heritability (Wallace et al., 2006; Lenroot et al., 2009). In a pediatric twin sample, the heritability of cortical thickness decreased with age in early developing brain areas, such as primary motor and sensory cortices, but increased with age in later-maturing areas, e.g., the prefrontal cortex (Lenroot et al., 2009) (see also Gogtay et al., 2004, for maps of the cortical maturational sequence). This was ascribed to the effects of age-dependent gene expression and the temporal variation in gene-environment correlations. Third, the current study is based on voxel-by-voxel analysis of diffusion images, in which regional characteristics of white matter fibers are summarized and assessed at a macroscopic scale (2 mm), but no actual tracking of white matter fibers was performed. Future studies using tractography (Wakana et al., 2004; Deriche and Descoteaux, 2007; Makris et al., 2007; Frey et al., 2008; Lenglet et al., 2008) may be able to answer questions about genetic influences on specific fiber pathways tracked in the images, such as the arcuate fasciculus or cingulum bundle, for example. Nevertheless, tract labeling is somewhat labor intensive at present, and the spatial scope of the tractography analysis can be somewhat limited, given the need to select fiber tracts of interest. Last, it may be oversimplified to use a scalar measure like FA to describe white matter architecture, as the directional information of water diffusion is not included. Future studies may be able to fit full multivariate structural equation models (Neale et al., 1992), to include the full diffusivity information in the diffusion tensors. However, this is very computationally expensive as the number of equations to solve is (2 × 6) × ((2 × 6) + 1) = 156 to fit the (a, c, e) parameters in the SEM for diffusion tensors.
In conclusion, we reported the first maps of genetic influences on fiber architecture in the living brain, based on a population study of diffusion tensor images. Major white matter fiber pathways are highly genetically controlled, and higher diffusion anisotropy was linked with superior intellectual performance in several key systems. These algorithms and results may help to guide future studies to detect individual genes contributing to fiber architecture, white matter integrity and cognition.
Footnotes
This work was supported by Grant RO1 HD050735 from the National Institute of Child Health and Human Development and Project Grant 496682 from the National Health and Medical Research Council, Australia. The collection of IQ data and zygosity typing was supported by the Australian Research Council (Grants A7960034, A79906588, A79801419, DP0212016). Additional support for algorithm development was provided by the National Institute on Aging, National Institute of Biomedical Imaging and Bioengineering, and the National Center for Research Resources (Grants AG016570, EB01651, RR019771 to P.M.T.). We are also extremely grateful to the twins for their willingness to participate in our studies, to the radiographer, Matt Meredith, Centre for Magnetic Resonance, University of Queensland, for image acquisition, and research nurses, Marlene Grace and Ann Eldridge, Queensland Institute of Medical Research, for twin recruitment.
References
- Aboitiz F. The origin of the mammalian brain as a case of evolutionary irreversibility. Med Hypotheses. 1992;38:301–304. doi: 10.1016/0306-9877(92)90021-4. [DOI] [PubMed] [Google Scholar]
- Alexander DC, Pierpaoli C, Basser PJ, Gee JC. Spatial transformations of diffusion tensor magnetic resonance. IEEE Trans Med Imaging. 2001;20:1131–1139. doi: 10.1109/42.963816. [DOI] [PubMed] [Google Scholar]
- Arbuthnott ER, Boyd IA, Kalu KU. Ultrastructural dimensions of myelinated peripheral nerve fibres in the cat and their relation to conduction velocity. J Physiol. 1980;308:125–157. doi: 10.1113/jphysiol.1980.sp013465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arsigny V, Fillard P, Pennec X, Ayache N. Fast and simple calculus on tensors in the log-Euclidean framework. Paper presented at the 8th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI); October; California: Palm Springs; 2005. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed. 2002;15:435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Begré S, Frommer A, von Känel R, Kiefer C, Federspiel A. Relation of white matter anisotropy to visual memory in 17 healthy subjects. Brain Res. 2007;1168:60–66. doi: 10.1016/j.brainres.2007.06.096. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. On the adaptive control of the false discovery rate in multiple testing with independent statistics. J Educ Behav Stat. 2000;25:60–83. [Google Scholar]
- Brown MB, Forsythe AB. Robust tests for the equality of variances. J Am Stat Assoc. 1974;69:364–367. [Google Scholar]
- Bush G, Luu P, Posner MI. Cognitive and emotional influences in anterior cingulate cortex. Trends Cogn Sci. 2000;4:215–222. doi: 10.1016/s1364-6613(00)01483-2. [DOI] [PubMed] [Google Scholar]
- Chiang MC, Dutton RA, Hayashi KM, Lopez OL, Aizenstein HJ, Toga AW, Becker JT, Thompson PM. 3D pattern of brain atrophy in HIV/AIDS visualized using tensor-based morphometry. Neuroimage. 2007;34:44–60. doi: 10.1016/j.neuroimage.2006.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiang MC, Leow AD, Klunder AD, Dutton RA, Barysheva M, Rose SE, McMahon KL, de Zubicaray GI, Toga AW, Thompson PM. Fluid registration of diffusion tensor images using information theory. IEEE Trans Med Imaging. 2008;27:442–456. doi: 10.1109/TMI.2007.907326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi SJ, Lim KO, Monteiro I, Reisberg B. Diffusion tensor imaging of frontal white matter microstructure in early Alzheimer's disease: a preliminary study. J Geriatr Psychiatry Neurol. 2005;18:12–19. doi: 10.1177/0891988704271763. [DOI] [PubMed] [Google Scholar]
- Christensen GE, Johnson HJ, Vannier MW. Synthesizing average 3D anatomical shapes. Neuroimage. 2006;32:146–158. doi: 10.1016/j.neuroimage.2006.03.018. [DOI] [PubMed] [Google Scholar]
- Deriche R, Descoteaux M. Splitting tracking through crossing fibers: multidirectional Q-ball tracking. Paper presented at Fourth IEEE International Symposium on Biomedical Imaging: From Nano to Macro (ISBI); April; Washington DC. 2007. [Google Scholar]
- de Zubicaray GI, Chiang MC, McMahon KL, Shattuck DW, Toga AW, Martin NG, Wright MJ, Thompson PM. Meeting the challenges of neuroimaging genetics. Brain Imaging Behav. 2008;2:258–263. doi: 10.1007/s11682-008-9029-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornell C, Larcker DF. Evaluating structural equation models with unobservable variables and measurement error. J Mark Res. 1981;18:39–50. [Google Scholar]
- Frangou S, Chitins X, Williams SC. Mapping IQ and gray matter density in healthy young people. Neuroimage. 2004;23:800–805. doi: 10.1016/j.neuroimage.2004.05.027. [DOI] [PubMed] [Google Scholar]
- Frey S, Campbell JS, Pike GB, Petrides M. Dissociating the human language pathways with high angular resolution diffusion fiber tractography. J Neurosci. 2008;28:11435–11444. doi: 10.1523/JNEUROSCI.2388-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogtay N, Giedd JN, Lusk L, Hayashi KM, Greenstein D, Vaituzis AC, Nugent TF, 3rd, Herman DH, Clasen LS, Toga AW, Rapoport JL, Thompson PM. Dynamic mapping of human cortical development during childhood through early adulthood. Proc Natl Acad Sci U S A. 2004;101:8174–8179. doi: 10.1073/pnas.0402680101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray JR, Thompson PM. Neurobiology of intelligence: science and ethics. Nat Rev Neurosci. 2004;5:471–482. doi: 10.1038/nrn1405. [DOI] [PubMed] [Google Scholar]
- Grayson DA. Twins reared together: minimizing shared environmental effects. Behav Genet. 1989;19:593–604. doi: 10.1007/BF01066256. [DOI] [PubMed] [Google Scholar]
- Haier RJ, Jung RE, Yeo RA, Head K, Alkire MT. Structural brain variation and general intelligence. Neuroimage. 2004;23:425–433. doi: 10.1016/j.neuroimage.2004.04.025. [DOI] [PubMed] [Google Scholar]
- Hedeker D, Gibbons RD, Flay BR. Random-effects regression models for clustered data with an example from smoking prevention research. J Consult Clin Psych. 1994;62:757–765. doi: 10.1037//0022-006x.62.4.757. [DOI] [PubMed] [Google Scholar]
- Hines M, Chiu L, McAdams LA, Bentler PM, Lipcamon J. Cognition and the corpus callosum: verbal fluency, visuospatial ability, and language lateralization related to midsagittal surface areas of callosal subregions. Behav Neurosci. 1992;106:3–14. doi: 10.1037//0735-7044.106.1.3. [DOI] [PubMed] [Google Scholar]
- Hoeft F, Barnea-Goraly N, Haas BW, Golarai G, Ng D, Mills D, Korenberg J, Bellugi U, Galaburda A, Reiss AL. More is not always better: increased fractional anisotropy of superior longitudinal fasciculus associated with poor visuospatial abilities in Williams syndrome. J Neurosci. 2007;27:11960–11965. doi: 10.1523/JNEUROSCI.3591-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes CJ, Hoge R, Collins L, Woods R, Toga AW, Evans AC. Enhancement of MR images using registration for signal averaging. J Comput Assist Tomogr. 1998;22:324–333. doi: 10.1097/00004728-199803000-00032. [DOI] [PubMed] [Google Scholar]
- Hopper JL, Visscher PM. Variance component analysis. In: Armitage P, Colton T, editors. Encyclopedia of biostatistics. 2nd Edition. Hoboken, NJ: Wiley Interscience; 2005. [Google Scholar]
- Hu X, Hicks CW, He W, Wong P, Macklin WB, Trapp BD, Yan R. Bace1 modulates myelination in the central and peripheral nervous system. Nat Neurosci. 2006;9:1520–1525. doi: 10.1038/nn1797. [DOI] [PubMed] [Google Scholar]
- Hulshoff Pol HE, Schnack HG, Posthuma D, Mandl RC, Baaré WF, van Oel C, van Haren NE, Collins DL, Evans AC, Amunts K, Bürgel U, Zilles K, de Geus E, Boomsma DI, Kahn RS. Genetic contributions to human brain morphology and intelligence. J Neurosci. 2006;26:10235–10242. doi: 10.1523/JNEUROSCI.1312-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson DN. MAB, multidimensional aptitude battery: manual. Port Hurton, Michigan: Research Psychologists; 1984. [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42:515–525. [PubMed] [Google Scholar]
- Jung RE, Haier RJ. The parieto-frontal integration theory (P-FIT) of intelligence: converging neuroimaging evidence. Behav Brain Sci. 2007;30:135–154. doi: 10.1017/S0140525X07001185. discussion 154–187. [DOI] [PubMed] [Google Scholar]
- Lange K, Boehnke M. Extensions to pedigree analysis. IV. Covariance components models for multivariate traits. Am J Med Genet. 1983;14:513–524. doi: 10.1002/ajmg.1320140315. [DOI] [PubMed] [Google Scholar]
- Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H. Diffusion tensor imaging: concepts and applications. J Magn Reson Imaging. 2001;13:534–546. doi: 10.1002/jmri.1076. [DOI] [PubMed] [Google Scholar]
- Lenglet C, Campbell J, Descoteaux M, Haro G, Savadjiev P, Wassermann D, Anwander A, Deriche R, Pike G, Sapiro G, Siddiqi K, Thompson P Advance online publication. Mathematical methods for diffusion MRI processing. Neuroimage. 2008 doi: 10.1016/j.neuroimage.2008.10.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenroot RK, Schmitt JE, Ordaz SJ, Wallace GL, Neale MC, Lerch JP, Kendler KS, Evans AC, Giedd JN. Differences in genetic and environmental influences on the human cerebral cortex associated with development during childhood and adolescence. Hum Brain Mapp. 2009;30:163–174. doi: 10.1002/hbm.20494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung LH, Ooi GC, Kwong DL, Chan GC, Cao G, Khong PL. White-matter diffusion anisotropy after chemo-irradiation: a statistical parametric mapping study and histogram analysis. Neuroimage. 2004;21:261–268. doi: 10.1016/j.neuroimage.2003.09.020. [DOI] [PubMed] [Google Scholar]
- Luciano M, Wright MJ, Geffen GM, Geffen LB, Smith GA, Evans DM, Martin NG. A genetic two-factor model of the covariation among a subset of Multidimensional Aptitude Battery and Wechsler Adult Intelligence Scale–Revised subtests. Intelligence. 2003;31:589–605. [Google Scholar]
- Luders E, Narr KL, Bilder RM, Thompson PM, Szeszko PR, Hamilton L, Toga AW. Positive correlations between corpus callosum thickness and intelligence. Neuroimage. 2007;37:1457–1464. doi: 10.1016/j.neuroimage.2007.06.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luders E, Narr K, Thompson P, Toga A Advance online publication. Neuroanatomical correlates of intelligence. Intelligence. 2008 doi: 10.1016/j.intell.2008.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makris N, Papadimitriou GM, Sorg S, Kennedy DN, Caviness VS, Pandya DN. The occipitofrontal fascicle in humans: a quantitative, in vivo, DT-MRI study. Neuroimage. 2007;37:1100–1111. doi: 10.1016/j.neuroimage.2007.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazziotta J, Toga A, Evans A, Fox P, Lancaster J, Zilles K, Woods R, Paus T, Simpson G, Pike B, Holmes C, Collins L, Thompson P, MacDonald D, Iacoboni M, Schormann T, Amunts K, Palomero-Gallagher N, Geyer S, Parsons L. A probabilistic atlas and reference system for the human brain: International Consortium for Brain Mapping (ICBM) Philos Trans R Soc Lond B Biol Sci. 2001;356:1293–1322. doi: 10.1098/rstb.2001.0915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDaniel MA. Big-brained people are smarter: a meta-analysis of the relationship between in vivo brain volume and intelligence. Intelligence. 2005;33:337–346. [Google Scholar]
- McGue M, Bouchard TJ., Jr Adjustment of twin data for the effects of age and sex. Behav Genet. 1984;14:325–343. doi: 10.1007/BF01080045. [DOI] [PubMed] [Google Scholar]
- McIntosh AM, Moorhead TW, Job D, Lymer GK, Muñoz Maniega S, McKirdy J, Sussmann JE, Baig BJ, Bastin ME, Porteous D, Evans KL, Johnstone EC, Lawrie SM, Hall J. The effects of a neuregulin 1 variant on white matter density and integrity. Mol Psychiatry. 2008;13:1054–1059. doi: 10.1038/sj.mp.4002103. [DOI] [PubMed] [Google Scholar]
- Miles DR, van den Bree MB, Pickens RW. Sex differences in shared genetic and environmental influences between conduct disorder symptoms and marijuana use in adolescents. Am J Med Genet. 2002;114:159–168. [PubMed] [Google Scholar]
- Mori S, Oishi K, Jiang H, Jiang L, Li X, Akhter K, Hua K, Faria AV, Mahmood A, Woods R, Toga AW, Pike GB, Neto PR, Evans A, Zhang J, Huang H, Miller MI, van Zijl P, Mazziotta J. Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. Neuroimage. 2008;40:570–582. doi: 10.1016/j.neuroimage.2007.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale MC, Miller MB. The use of likelihood-based confidence intervals in genetic models. Behav Genet. 1997;27:113–120. doi: 10.1023/a:1025681223921. [DOI] [PubMed] [Google Scholar]
- Neale MC, Cardon LR the NATO Scientific Affairs Division. Methodology for genetic studies of twins and families. Dordrecht, the Netherlands/Boston: Kluwer Academic; 1992. [Google Scholar]
- Park HJ, Kubicki M, Shenton ME, Guimond A, McCarley RW, Maier SE, Kikinis R, Jolesz FA, Westin CF. Spatial normalization of diffusion tensor MRI using multiple channels. Neuroimage. 2003;20:1995–2009. doi: 10.1016/j.neuroimage.2003.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfefferbaum A, Sullivan EV, Carmelli D. Genetic regulation of regional microstructure of the corpus callosum in late life. Neuroreport. 2001;12:1677–1681. doi: 10.1097/00001756-200106130-00032. [DOI] [PubMed] [Google Scholar]
- Posthuma D, De Geus EJ, Baaré WF, Hulshoff Pol HE, Kahn RS, Boomsma DI. The association between brain volume and intelligence is of genetic origin. Nat Neurosci. 2002;5:83–84. doi: 10.1038/nn0202-83. [DOI] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes in C++ Ed 2. Cambridge: Cambridge UP; 2002. [Google Scholar]
- Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49:177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- Schmithorst VJ, Wilke M, Dardzinski BJ, Holland SK. Cognitive functions correlate with white matter architecture in a normal pediatric population: a diffusion tensor MRI study. Hum Brain Mapp. 2005;26:139–147. doi: 10.1002/hbm.20149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt JE, Wallace GL, Rosenthal MA, Molloy EA, Ordaz S, Lenroot R, Clasen LS, Blumenthal JD, Kendler KS, Neale MC, Giedd JN. A multivariate analysis of neuroanatomic relationships in a genetically informative pediatric sample. Neuroimage. 2007;35:70–82. doi: 10.1016/j.neuroimage.2006.04.232. [DOI] [PubMed] [Google Scholar]
- Schmitt JE, Lenroot R, Ordaz SE, Wallace GL, Lerch JP, Evans AC, Prom EC, Kendler KS, Neale MC, Giedd JN Advance online publication. Variance decomposition of MRI-based covariance maps using genetically informative samples and structural equation modeling. Neuroimage. 2008a doi: 10.1016/jneuroimage.2008.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt JE, Lenroot RK, Wallace GL, Ordaz S, Taylor KN, Kabani N, Greenstein D, Lerch JP, Kendler KS, Neale MC, Giedd JN. Identification of genetically mediated cortical networks: a multivariate study of pediatric twins and siblings. Cereb Cortex. 2008b;18:1737–1747. doi: 10.1093/cercor/bhm211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeman E, Hopper JL, Young NR, Formica C, Goss P, Tsalamandris C. Do genetic factors explain associations between muscle strength, lean mass, and bone density? A twin study. Am J Physiol. 1996;270:E320–E327. doi: 10.1152/ajpendo.1996.270.2.E320. [DOI] [PubMed] [Google Scholar]
- Shattuck DW, Chiang M-C, Barysheva M, McMahon KL, de Zubicaray GI, Meredith M, Wright MJ, Toga AW, Thompson PM. Visualization tools for high angular resolution diffusion imaging. Paper presented at the 11th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI); September; New York, New York. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, Watkins KE, Ciccarelli O, Cader MZ, Matthews PM, Behrens TE. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31:1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Storey JD, Tibshirani R. Statistical significance for genomewide studies. Proc Natl Acad Sci U S A. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson PM, Cannon TD, Narr KL, van Erp T, Poutanen VP, Huttunen M, Lönnqvist J, Standertskjöld-Nordenstam CG, Kaprio J, Khaledy M, Dail R, Zoumalan CI, Toga AW. Genetic influences on brain structure. Nat Neurosci. 2001;4:1253–1258. doi: 10.1038/nn758. [DOI] [PubMed] [Google Scholar]
- Toga AW, Thompson PM. Genetics of brain structure and intelligence. Annu Rev Neurosci. 2005;28:1–23. doi: 10.1146/annurev.neuro.28.061604.135655. [DOI] [PubMed] [Google Scholar]
- Tyszka JM, Readhead C, Bearer EL, Pautler RG, Jacobs RE. Statistical diffusion tensor histology reveals regional dysmyelination effects in the shiverer mouse mutant. Neuroimage. 2006;29:1058–1065. doi: 10.1016/j.neuroimage.2005.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ukoumunne OC. A comparison of confidence interval methods for the intraclass correlation coefficient in cluster randomized trials. Stat Med. 2002;21:3757–3774. doi: 10.1002/sim.1330. [DOI] [PubMed] [Google Scholar]
- Urbanski M, Thiebaut de Schotten M, Rodrigo S, Catani M, Oppenheim C, Touze E, Chokron S, Méder JF, Lévy R, Dubois B, Bartolomeo P. Brain networks of spatial awareness: evidence from diffusion tensor imaging tractography. J Neurol Neurosurg Psychiatry. 2008;79:598–601. doi: 10.1136/jnnp.2007.126276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakana S, Jiang H, Nagae-Poetscher LM, van Zijl PC, Mori S. Fiber tract-based atlas of human white matter anatomy. Radiology. 2004;230:77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- Wallace GL, Eric Schmitt J, Lenroot R, Viding E, Ordaz S, Rosenthal MA, Molloy EA, Clasen LS, Kendler KS, Neale MC, Giedd JN. A pediatric twin study of brain morphometry. J Child Psychol Psychiatry. 2006;47:987–993. doi: 10.1111/j.1469-7610.2006.01676.x. [DOI] [PubMed] [Google Scholar]
- Wiesel TN, Hubel DH. Effects of visual deprivation on morphology and physiology of cells in the cats lateral geniculate body. J Neurophysiol. 1963;26:978–993. doi: 10.1152/jn.1963.26.6.978. [DOI] [PubMed] [Google Scholar]
- Wilke M, Sohn JH, Byars AW, Holland SK. Bright spots: correlations of gray matter volume with IQ in a normal pediatric population. Neuroimage. 2003;20:202–215. doi: 10.1016/s1053-8119(03)00199-x. [DOI] [PubMed] [Google Scholar]
- Yoshiura T, Mihara F, Ogomori K, Tanaka A, Kaneko K, Masuda K. Diffusion tensor in posterior cingulate gyrus: correlation with cognitive decline in Alzheimer's disease. Neuroreport. 2002;13:2299–2302. doi: 10.1097/00001756-200212030-00026. [DOI] [PubMed] [Google Scholar]
- Yu C, Li J, Liu Y, Qin W, Li Y, Shu N, Jiang T, Li K. White matter tract integrity and intelligence in patients with mental retardation and healthy adults. Neuroimage. 2008;40:1533–1541. doi: 10.1016/j.neuroimage.2008.01.063. [DOI] [PubMed] [Google Scholar]






