0.999...: Difference between revisions
creating page: some content copied from en:0.999... |
0$ Tags: Visual edit Mobile edit Mobile web edit |
||
| (46 intermediate revisions by 37 users not shown) | |||
| Line 1: | Line 1: | ||
| ⚫ | |||
'''0.999...''' is one of the ways [[1 (number)|the number 1]] can be written. |
|||
'''0.999...''' (also written as 0.{{overline|9}} or 0.{{overset|.|9}}, and read as "0 point 9 repeating") is one of the ways the number [[1 (number)|1]] (one) can be written. Even though it is written like this, no matter how many nines there are before the [[ellipsis]], it is still equal in value to 1. |
|||
==About== |
== About == |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
0.999... can also be written as |
|||
| ⚫ | It is hard for many people to understand why |
||
<math alt="0.9 with bar over the 9" style="position:relative;top:-.35em">0.\bar{9}</math> or |
|||
<math alt="0.9 with dot over the 9" style="position:relative;top:-.35em">0.\dot{9}</math>. |
|||
| ⚫ | It is hard for many people to understand why 0.999... is the same as 1. There are many [[mathematical proof|proofs]] that show why they are the same number, but many of these proofs are very complex.<ref name="Katz">{{cite journal |last1=Katz |first1=K. |last2=Katz |first2=M. |author2-link=Mikhail Katz |year=2010a |title=When is .999... less than 1? |journal=The Montana Mathematics Enthusiast |volume=7 |issue=1 |pages=3–30 |doi=10.54870/1551-3440.1381 |s2cid=11544878 |url=http://www.math.umt.edu/TMME/vol7no1/ |access-date=2010-10-17 |archive-date=2011-07-20 |archive-url=https://web.archive.org/web/20110720095125/http://www.math.umt.edu/TMME/vol7no1/ |url-status=dead }}</ref> |
||
==Proof== |
|||
| ⚫ | |||
== Examples == |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | When 1 is divided by 3, the answer is <math>1/3</math>. Since the answers are the same, that means that 0.999... and 1 are the same. Another way of thinking about it is if <math>1/3=0.333\ldots</math> and <math>2/3=0.666\ldots</math>, then <math>3/3=0.999\ldots</math> therefore, as <math>3/3=1</math>, 0.999... must also equal 1. There are many other ways of showing this.<ref name="Katz" /> |
||
| ⚫ | |||
Another way of proving that 0.999... = 1 is by accepting the simple fact that if two numbers are different, there must be at least one number between them. For example, a number between 1 and 2 is 1.5, and a number between 0.9 and 1 is 0.95. Since 0.999... has an [[Infinity|infinite]] number of 9s, there cannot be another number after the "last" 9, meaning there is no number between 0.999... and 1. Therefore, they are equal. |
|||
One more common proof is such: |
|||
<math>x=0.999\ldots</math> |
|||
<math>10x=9.999\ldots</math> |
|||
<math>10x-x=9.999\ldots-x</math> |
|||
<math>9x=9.999\ldots-0.999\ldots=9</math> |
|||
<math>x=9/9</math> |
|||
<math>x=1</math> |
|||
<math>0.999\ldots=1</math> |
|||
== In popular culture == |
|||
As the [[Internet]] developed, arguments about 0.999... are often on [[newsgroup]]s and [[message board]]s. Even newsgroups and message boards that do not have much to do with math argue about this. In the newsgroup sci.math, arguing about 0.999... is a "popular sport".<ref name=sci.mathfaq/> It is also one of the questions in its [[FAQ]].<ref name=sci.mathfaq>As observed by Richman (p. 396). {{cite web |url=http://www.faqs.org/faqs/sci-math-faq/specialnumbers/0.999eq1/ |author=Hans de Vreught | year=1994 | title=sci.math FAQ: Why is 0.9999... = 1? |access-date=2006-06-29}}</ref> |
|||
== Related pages == |
|||
* [[Limit (mathematics)]] |
|||
| ⚫ | |||
{{reflist}} |
{{reflist}} |
||
==Other websites== |
== Other websites == |
||
* [http://mathforum.org/dr.math/faq/faq.0.9999.html Why does 0.9999... = 1 |
* [http://mathforum.org/dr.math/faq/faq.0.9999.html Why does 0.9999... = 1?] |
||
* [http://www.newton.dep.anl.gov/askasci/math99/math99167.htm Ask A Scientist: Repeating Decimals] |
* [http://www.newton.dep.anl.gov/askasci/math99/math99167.htm Ask A Scientist: Repeating Decimals] {{Webarchive|url=https://web.archive.org/web/20150226225642/http://newton.dep.anl.gov/askasci/math99/math99167.htm |date=2015-02-26 }} |
||
* [ |
* [https://betterexplained.com/articles/a-friendly-chat-about-whether-0-999-1/ A Friendly Chat About Whether 0.999... = 1] |
||
[[Category:Mathematics]] |
[[Category:Mathematics]] |
||
[[ar:0.999...]] |
|||
{{math-stub}} |
|||
[[be:0,(9)]] |
|||
[[be-x-old:0,(9)]] |
|||
[[bg:0,(9)]] |
|||
[[ca:0,999...]] |
|||
[[da:0,999...=1]] |
|||
[[de:Eins#Periodischer Dezimalbruch]] |
|||
[[el:0,999...]] |
|||
[[en:0.999...]] |
|||
[[es:0,9 periódico]] |
|||
[[eo:0,999...]] |
|||
[[fa:۰٫۹۹۹…]] |
|||
[[fr:Développement décimal de l'unité]] |
|||
[[ko:0.999…]] |
|||
[[id:0,999...]] |
|||
[[it:0,999...]] |
|||
[[he:0.999...]] |
|||
[[ka:0,(9)]] |
|||
[[lv:0,999...]] |
|||
[[hu:0,999…]] |
|||
[[ml:0.999...]] |
|||
[[ms:0.999...]] |
|||
[[nl:Repeterende breuk#Repeterende negens]] |
|||
[[ja:0.999...]] |
|||
[[no:0,999...]] |
|||
[[nov:0.999...]] |
|||
[[uz:0,(9)]] |
|||
[[pl:0,(9)]] |
|||
[[pt:0,999...]] |
|||
[[ro:0,(9)]] |
|||
[[ru:0,(9)]] |
|||
[[sq:0.999...]] |
|||
[[sl:0,999...]] |
|||
[[fi:0,999...]] |
|||
[[sv:0,999...]] |
|||
[[ta:0.999...]] |
|||
[[th:0.999...]] |
|||
[[tr:0,999...]] |
|||
[[vi:0,999...]] |
|||
[[yo:0.999...]] |
|||
[[zh:0.999…]] |
|||
Latest revision as of 04:34, 1 July 2024
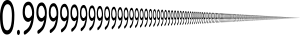
0.999... (also written as 0.9 or 0., and read as "0 point 9 repeating") is one of the ways the number 1 (one) can be written. Even though it is written like this, no matter how many nines there are before the ellipsis, it is still equal in value to 1.
About
[change | change source]0.999... is a repeating decimal, which means the digit "9" is repeated forever. It is different from 0.999, which only has three 9s.
0.999... can also be written as or .
It is hard for many people to understand why 0.999... is the same as 1. There are many proofs that show why they are the same number, but many of these proofs are very complex.[1]
Examples
[change | change source]One simple way of showing that 0.999... and 1 are the same thing is to divide them both by the number 3. When 0.999... is divided by 3, the answer is 0.333..., which is the same as (the fraction one third).
When 1 is divided by 3, the answer is . Since the answers are the same, that means that 0.999... and 1 are the same. Another way of thinking about it is if and , then therefore, as , 0.999... must also equal 1. There are many other ways of showing this.[1]
Another way of proving that 0.999... = 1 is by accepting the simple fact that if two numbers are different, there must be at least one number between them. For example, a number between 1 and 2 is 1.5, and a number between 0.9 and 1 is 0.95. Since 0.999... has an infinite number of 9s, there cannot be another number after the "last" 9, meaning there is no number between 0.999... and 1. Therefore, they are equal.
One more common proof is such:
In popular culture
[change | change source]As the Internet developed, arguments about 0.999... are often on newsgroups and message boards. Even newsgroups and message boards that do not have much to do with math argue about this. In the newsgroup sci.math, arguing about 0.999... is a "popular sport".[2] It is also one of the questions in its FAQ.[2]
Related pages
[change | change source]References
[change | change source]- ↑ 1.0 1.1 Katz, K.; Katz, M. (2010a). "When is .999... less than 1?". The Montana Mathematics Enthusiast. 7 (1): 3–30. doi:10.54870/1551-3440.1381. S2CID 11544878. Archived from the original on 2011-07-20. Retrieved 2010-10-17.
- ↑ 2.0 2.1 As observed by Richman (p. 396). Hans de Vreught (1994). "sci.math FAQ: Why is 0.9999... = 1?". Retrieved 2006-06-29.
Other websites
[change | change source]- Why does 0.9999... = 1?
- Ask A Scientist: Repeating Decimals Archived 2015-02-26 at the Wayback Machine
- A Friendly Chat About Whether 0.999... = 1