Abstract
Denoising, skull stripping, segmentation, feature extraction, and classification are five important processes in this paper’s development of a brain tumor classification model. The brain tumor image will be imposed first using the entropy-based trilateral filter to de-noising and this image is imposed to skull stripping by means of morphological partition and Otsu thresholding. Adaptive contrast limited fuzzy adaptive histogram equalization (CLFAHE) is also used in the segmentation process. The gray-level co-occurrence matrix (GLCM) characteristics are derived from the segmented image. The collected GLCM features are used in a hybrid classifier that combines the neural network (NN) and deep belief network (DBN) ideas. As an innovation, the hidden neurons of the two classifiers are modified ideally to improve the prediction model’s accuracy. The hidden neurons are optimized using a unique hybrid optimization technique known as lion with dragonfly separation update (L-DSU), which integrates the approaches from both DA and LA. Finally, the suggested model’s performance is compared to that of the standard models concerning certain performance measures.
Keywords: Brain tumor, Otsu thresholding and morphological segmentation, CLAFAHE, GLCM, DBN and NN, L-DSU
Introduction
Nowadays, the life expectancy rate of humans is diminishing deeply due to brain tumors as it affects all ages of humans, whether it be a child or an adult or an old-age person [1–5]. In general, a brain tumor is defined as a solid lesion due to abnormal cell proliferation; the brain tumor’s symptoms differ from person to person depending on the tumor’s location [6, 7]. Primary brain tumor and secondary brain tumor are the two types of brain tumors. The intracranial tumor generated within the brain is said to be primary brain tumors; the benign and malignant types fall under this section [8–11]. The benign brain tumors originate within the brain and they are non-cancerous as they do not affect certain other regions of the body. Brain tumors that are malignant can extend to other body parts, including the spine [12, 13].
Further, while compared to benign, the malignant tumors are faster in spreading and the growth rate of the cancerous cell is also high. The diagnosis, as well as treatment of the benign brain tumor, is quite easier than the malignant tumor as they have defined boundaries and are not deeply buried within the brain [14, 15]. The most common type of primary tumor is gliomas, and they are created by glial cells, which are the brain’s supporting structures. On the other hand, the tumors that do not originate within the brain and get to spread to the brain via different body parts are referred to as the second brain tumor and this process of spreading of the tumor is said to be metastasis [16–18]. The naming of the second type of tumor is done on the basis of the parts from which the tumor originates and metastatic lung tumor refers to the brain tumor that originates from the lungs.
In the human brain, the tumor regions, as well as other accidental damages, are diagnosed by researchers as well as radiologists with brain imaging techniques [19–21]. MRI and CT scans are now the most routinely used procedures for diagnosing brain tumors. While compared to CT, the MRI has the capability of indicating the origin of the tumor and has a higher resolution in detecting the heterogeneity within tumors [22]. The patient’s survival rate can usually be increased if the tumor’s origin, stage, and classification are discovered at an earlier stage with more precision. But, it is complex to detect the tumors overlapped within the dense brain tissues with the help of brain imaging techniques alone. This might lead to misdiagnosis of location and volume due to human errors generated by visual fatigue. As a result, the development of an automatic brain tumor categorization technique is required in order to reduce the load of the human observer and to enhance the accuracy of the diagnosis under the large number of images.
Recently, there is endless research being carried out in brain image classification, among which ANN is faster in computation and has reduced the expert intervention during the whole diagnosis process [23]. The major shortcoming of this model lies in training as well as the learning process, as both are tedious processes. Further, to get a better segmentation quality, the fuzzy C-means algorithm is employed; this model is more robust to noise and it is deeply stuck within the consideration of the image intensity values. Further, SVM works effectively in high-dimensional feature spaces and is unaffected by the dimensionality of the feature space. But, this technique is not utilized commonly as it is extremely reliant upon the data size. The real-time image segmentation is accomplished with the KNN algorithm as it is faster and it is more prone to yielding erroneous decisions. Thus, there is a necessity to develop a more flexible technique that can classify brain tumors accurately and preciously. The goal of this project is to improve physicians’ perceptions of targeted things (i.e., brain tumors), which is problematic for a variety of reasons, including a lack of detection accuracy. The goal of the approach discussed in this study was to create an efficient framework that integrates the properties of the Dragonfly and Lion algorithms to solve the constraints of the current brain tumor classification system.
The following are the contributions of the current research effort on brain tumor classification:
A brain tumor classification model is developed by following five major steps, namely denoising, skull stripping, segmentation, feature extraction, and classification.
The brain tumor image from the MRI dataset is de-noised using an entropy-based trilateral filter, and the de-noised picture is again processed to Otsu thresholding and morphological segmentation.
Adaptive CLFAHE is then used to do the segmentation process.
GLCM characteristics are extracted from the segmented picture. The retrieved GLCM features are classified using a hybrid classifier that combines the concepts of DBN and NN.
The hidden neurons of the classifiers (DBN and NN) have been ideally optimized using a novel hybrid optimization approach called L-DSU to make the prediction model more exact.
Finally, the L-DSU’s performance is evaluated to that of traditional models on a number of performance metrics.
The parts of this research study are structured as follows: A concise summary of the literary works that have been conducted on this topic is discussed in “Literature Review”. The proposed brain tumor classification paradigm is described in “Proposed Brain Tumor Classification Model: Architectural Explanation.” “Image Denoising and Skull Stripping: Procedural Explanation” depicts the suggested image denoising and skull stripping: procedural explanation. Further, segmentation via adaptive CLFAHE-based contrast enhancement and GLCM-based feature extraction is explained in “Segmentation via Adaptive CLFAHE-Based Contrast Enhancement and GLCM-Based Feature Extraction.” In “Introduction of Hybrid Classifier: DBN and NN,” DBN and NN are explored. In addition, “Proposed Hybrid Algorithm for Hybrid Classifier Optimization: Objective Function and Solution Encoding” depicts the suggested hybrid algorithm for hybrid classifier optimization: objective function and solution encoding. The obtained results are discussed in “Result and Discussion” and the final section of this study project delivers a solid conclusion.
Literature Review
Related Works
In 2018, Ma et al. [24] established the RF-MPDAC model technique for automated segmentation of the brain tumor images from multimodal volumetric MR images. This model has combined both the active contour model and random forests. The modality-specific random forests were employed with the intent of exploring the contextual as well as local information from multimodal images and the random forest integrated different levels of structural information for glioma structure interference. In order to refine the glioma structures, the multiscale patch-driven active contour model was projected, taking into account the advantage of sparse representation methodologies.
In 2016, Anitha and Murugavalli [25] developed a two-tier classification technique using an adaptive pillar K-means algorithm to segment and classify brain tumors from MR images. The features retrieved from the discrete wavelet transform are trained via a self-organizing map neural network and the K-nearest neighbor was used to train the resultant filter factors at the same time.
In 2019, Hemanth et al. [26] designed a novel MDCNN for the classification of MR brain images collected from patients with brain tumors. By reducing the number of training photos, this model accurately identified schizophrenia.
In 2019, Hemanth and Anitha [27] suggested a unique image classification method for classifying aberrant MR brain tumor pictures using modified GA. GLDM was used to retrieve texture features from the image, and the modified GA method was used to retrieve the most relevant features from the image. The suggested model was compared to traditional models in terms of PPV, accuracy, specificity, and sensitivity after the retrieved optimal features were classified using BPN.
In 2019, Rehman et al. [28] formulated an automatic brain tissue classification method for the categorization of both the normal and the pathological tissues based on an RF-based regional classifier. Statistically, text on histograms and fractal features were retrieved from the image in this step. Further, the proposed approach worked well in simultaneous brain tumor detection and segmentation.
In 2019, Chen et al. [29] introduced a new multi-layer perceptron-based post-processing technique for detecting brain tumors. This is accomplished by substituting the DeepMedic model used in segmentation with Multi-Level DeepMedic, which utilizes multi-level data. An innovative dual-force training approach improved the quality of the multilevel characteristics. The image classifications were also done with the help of an auxiliary classifier.
In 2018, Bal et al. [30] proposed RFCM in accordance with shape-based topological properties as an innovative technique for automated brain tumor segmentation. Fuzzy membership was used to effectively solve the overlapping partition difficulties in rough-fuzzy C-means, and the upper and lower bounds of rough sets were used to handle the dataset’s uncertainties. In the brain tumor segmentation, the crisp lower approximation, as well as the fuzzy boundary belonging to RFCM, was efficient. The skull stripping was accomplished via the patch-based K-means method.
In 2018, Pinto et al. [31] have established an automatic hierarchical brain tumor segmentation pipeline by an innovative technology referred to as ERT, which was associated with context-based features. Initially, the location, as well as the shape of the tumor, was evaluated and the tumor region was classified into varying types of tumor tissues by hierarchical two-stage classification.
Review
The literature works on brain tumor diagnosis are depicted in Table 1, in which different techniques and features concerning each research work are exhibited. It is vivid that beyond the advantages, there are still some shortcomings, and hence, it requires further research in this area. In the RF-MPDAC technique, the accuracy of classification is high and the computational complexity is low. The model’s primary problem is it requires a vast count of labeled training data [24]. In the adaptive pillar K-means clustering algorithm, the correlation between the images is lowered, and the main obstacles are poor computational speed and specificity [25]. MDCNN has enhanced TPR as well as TNR and has reduced the computational complexity. Apart from this, a large dataset is required for training and hence it is computationally complex [26]. GA with BPN has reduced the count of the features and hence the accuracy in classification is high. But, here, the complexity and error rates are high [27]. The tumor regions were localized accurately and the feature matrix is imbalanced [28]. In the multi-layer perceptron-based post-processing approach [29], high-level semantic Information was described accurately and the computational cost is low. The major drawback of this model is high computational complexity due to the requirement of a huge set of features. RFCM [31] is efficient in handling the issues of uncertainty and overlapping partitions in the datasets and it suffers from the drawback of high computations ERT is a multi-class, computationally efficient, and high-dimensional feature vector-handling algorithm. The major disadvantage of this model lies in low sensitivity as well as specificity.
Table 1.
Feature and difficulties of brain tumor diagnosis models
| Author | Method | Features | Difficulties |
|---|---|---|---|
| Ma et al. [24] | RF-MPDAC |
• High accuracy • Low computational complexity |
• Requires a vast count of labeled training data • The outputs of the algorithms systematically influence the ground truth labels |
| Anitha and Murugavalli [25] | Adaptive pillar K-means clustering algorithm |
• Faster in determining the correlation between images • Simplest technique |
• Low computational speed and specificity |
| Hemanth et al. [26] | MDCNN |
• True positive and true negative rates are higher • Low computational complexity |
• Requires large dataset for training • High complexity |
| Hemanth and Anitha [27] | GA with BPN | • Count of features is minimized | • High complexity and high error rate |
| Rehman et al. [28] | RF-based regional classifier | • Accurate localization of tumor regions |
• Failure to capture tumor boundaries • Feature matrix is imbalanced |
| Chen et al. [29] | Multi-layer perceptron based post-processing approach |
• Accurate description of high-level semantic Information • Low computational cost |
• Requires large dataset for training |
| Bal et al. [30] | RFCM | • Handle the datasets uncertainty and overlapping partitions | • High computational complexity |
| Pinto et al. [31] | ERT |
• Multi-class in nature • Capable of handling high dimensional feature vectors • Computationally efficient |
• Low sensitivity and specificity |
Problem Definition
From Table 1, it is clear that besides the benefits, there are certain flaws requiring additional research in this field. The high computing complexity of many approaches is a key disadvantage. For illustration, computational complexity is high in MDCNN [26], GA with BPN approach [27], and RFCM techniques [30]. Another significant drawback is that training requires a large number of datasets. The problems of requiring a high number of datasets for training are encountered in the MDCNN methodology [26] and in the multi-layer perceptron-based post-preprocessing technique [29]. The limitation of the RF-MPDAC technique [24] is that the ground truth tables are systematically influenced by the algorithm outputs. In the adaptive pillar K-means clustering technique [25], the correlation between the images is minimized, and the main obstacles are poor computational speed and specificity. The RF-based regional classifier technique [28] fails to capture tumor boundaries and the feature matrix is imbalanced. On the other hand, the proposed model resolves the issues with the RF-based regional classifier technique [28]. The disadvantage of the ERT approach [31] is its low sensitivity and specificity.
Proposed Brain Tumor Classification Model: Architectural Explanation
The purpose of the study is really to create a coronal view image-based brain tumor classification model, which is illustrated in Fig. 1. Denoising, skull stripping, segmentation, feature extraction, and classification are the phases assigned to this model. The entropy-based trilateral filter (EnTri filter) is used to de-noise the brain tumor image from the MRI dataset, and the filtered images are then subjected to skull stripping by Otsu thresholding as well as morphological segmentation. Following that, adaptive CLFAHE is employed to perform the segmentation process. The segmented image is then used to extract GLCM features. The hybridized NN and DBN are used to classify the selected optimal GLCM features. As a major contribution, the newly hybridized optimization algorithm aids in optimizing the hidden neurons in both NN and DBN and hence enhances the accuracy of classification and the proposed hybrid optimization algorithm is referred to as L-DSU.
Fig. 1.
Block diagram of the proposed brain tumor classification model
Image Denoising and Skull Stripping: Procedural Explanation
Image Denoising
Entropy-Based Bilateral Filter [32]
The bilateral filters for the edge preserved denoising formed by the combination of the range filtering with the domain filtering is the inspiration behind the development of the EnTri filter. Here, the new range of filters that integrates the weighting function with the adaptive median filter is expressed as per Eq. (1). The median metric component and the median intensity are acquired with the help of initializing the modified adaptive median filter from the greatest limit neighborhood to the subsequent location . is the intensity value at the given position and be the location of the pixel under consideration
| 1 |
Then, the entropy function is formulated as per Eq. (2) to tackle the impulse noise in input photographic images. The probability can be defined as per Eq. (3). In addition, the disparity existing in between and is depicted as and it can be expressed mathematically as per Eq. (4). The absolute value and the maximum possible pixel value of the image are expressed by and , respectively. Further, in between the radiometric components and median-metric components, the weight is adaptively adjusted with the entropy function expressed in Eq. (5).
| 2 |
where the probability at is defined as,
| 3 |
where is the disparity between M and ,
| 4 |
| 5 |
As a whole, EnTri is nothing but the weighting of every pixel via normalization and this is shown mathematically as per Eq. (6).
| 6 |
The input image is de-noised and then subjected to skull stripping and segmented.
Skull Stripping Process
The denoised image is fed into the skull stripping procedure, and the denoised image is processed using Otsu thresholding and morphological segmentation. A brief description of the Otsu thresholding is depicted below:
Otsu Thresholding [33]
It belongs to the linear discriminant criteria and here the objects in the image consider the only background and reject the heterogeneity and diversity corresponding to the background. The threshold is set by the Otsu set with the objective of alleviating the overlapping in class distributions. Given this definition, “Otsu’s method splits the image into two light and dark parts and , where the region is a set notation and region ”. Here, the term indicates the threshold value and 1 is the image maximum gray level. Further, and can be used for both the object and the background or conversely. Further, the availability of all the possible threshold values is scanned and on each side of the threshold, the minimum value of the pixels is computed. Further, the major intention of Otsu thresholding is to compute the minimum entropy for the sum of background and foreground. The sum total of the weighted group variance is diminished to compute the optimal threshold value. For the observed grayscale value , the histogram probability is represented as . In the image, the index for row and column is indicated using the terms , respectively. Further, in the same image, the count of the rows and columns is symbolized as , respectively.
| 7 |
The class having the intensity ranging from 0 to , the weight, mean, and variance are depicted using the term , , and , respectively. In addition, the class lying in between to 1 in terms of intensity has the weight as , mean as , and variance . The term denotes the weighted sum of group variances and it is stated mathematically as Eq. (8). The best threshold is depicted as and it has the minimum value within the class variance. The within-class variables are defined mathematically as per Eqs. (9)–(14).
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
Morphology Segmentation [34]
Morphological segmentation is a rich framework for segmenting images as well as video sequences. It is based on the set theory and the logical operations that are quite easier to be utilized. In general, the two major morphological operations are erosion and dilation. The opening operation is accomplished with respect to these two operations.
Opening: The opening of the image is nothing but the linking of both the erosion and dilation operations. With the help of Eq. (15), element B structures the opening of image A. The relationship between opening, erosion, and dilation is defined by this statement. This phrase clearly depicts that the picture opening is the result of the image being destroyed by a structural feature, which also aids in the dilation of the resulting erosion image. The point at which the structured element that rolled roughly within this boundary and reaches the extreme points within this boundary is specified as the boundary of the opened image. Further, the union set operation helps in determining the points of the opened image.
| 15 |
These opening operations reject the minor extensions of the object and smoothen the outline in addition to narrow bridge clearance.
Segmentation via Adaptive CLFAHE-based Contrast Enhancement and GLCM-based Feature Extraction
Adaptive CLFAHE
The skull stripped image is subjected to CLFAHE for the segmentation of the image. CLFAHE [35] encloses three major stages, such as image fuzzification, alteration of membership function values, and defuzzification. These fuzzy rules give directives much similar to human-like reasoning and it treats the images as a fuzzy set and operates on those sets. The steps involved in the novel CLFAHE model are described in the subsequent section:
Read the stripped image of a skull.
Convert the skull stripped picture into a grayscale image, if it is in RGB format.
Then, compute the size of the grayscale image .
Add noise to the grayscale image.
Then, from the noised grayscale image, the gray level is determined in addition to its minimum and maximum value.
The image is then cropped, then the newly formed (cropped) image is denoted by .
- The image function is computed using Eq. (18), in which the minimum gray is , and maximum gray as well as any gray level is depicted by and , respectively.
18 -
With the aid of the membership modification, the whole pixels are explained.
then19
or20
then21 22 The maximum, minimum, and medium bounding limits are 1, 0, and 0.5, respectively.
Show the resultant image.
Extraction of GLCM Feature
The GLCM characteristics are extracted after segmentation. Probably one of the best statistical methods for extracting texture from pictures is the GLCM [36] approach. Some of the properties generated from the image include contrast, entropy, mean, correlation, variance, SD, cluster proximity, energy and homogeneity, dissimilarity, and maximum probability. Table 2 shows the typical GLCM characteristics. The features retrieved from GLCM are .
Table 2.
GLCM features
| Contrast |
where ➜ element in the co-occurrence matrix at the coordinates and ➜ dimension of the co-occurrence matrix |
| Correlation |
where and ➜ standard deviation |
| Entropy | |
| Energy | |
| Homogeneity | |
| Mean | |
| Variance | |
| Standard Deviation | |
| Dissimilarity | |
| Maximum Probability | |
| Cluster Prominence |
Introduction of Hybrid Classifier: DBN and NN
The extracted GLCM features are subjected to the hybrid classifier.
A. DBN
DBN [37, 38] was introduced in the year 2018 by Smolensky with multiple layers. The input layer includes visible neurons, while the output layer contains hidden neurons. Between the hidden and the visible neurons, there is an exclusive and also symmetric link. Furthermore, there is no relation among the input neurons as well as the hidden neurons, which is a distinguishing property of DBN. The Boltzmann networks with stochastic neurons exhibit the outcome , which is probabilistic in nature and has a probability function as per Eq. (23). Further, the mathematical expression for is provided in Eq. (24), where the notation is the pseudo-temperature that transforms the stochastic model into a deterministic model when it reaches 0.
Boltzmann Machine
The computation of the energy of the Boltzmann machine takes place in the configured neuron state according to Eq. (26). The weight between neurons and is denoted by ; the term and are the biases and binary state of neurons, respectively.
| 23 |
| 24 |
| 25 |
| 26 |
The influence of a single-unit state on global energy is computed using Eq. (27). The gradient descends mechanism in the system aids in discovering the lowest feasible energy in the training process for the given input.
| 27 |
Restricted Boltzmann Machine
It is not the same as a regular Boltzmann machine, and the only distinction is that during the computation of the energy difference between visible and hidden neurons, restricted Boltzmann machine (RBM) does not rely on visible or hidden neurons. Equations (28), (29) and (30) represent the energy definitions of visible and hidden neurons relating to joint composition.
| 28 |
| 29 |
| 30 |
The binary state and visible unit bias are denoted as and , respectively. The weight among the neurons is represented as . Additionally, the binary state and bias of hidden units are denoted as and , respectively.
RBM Training
For RBM training, unsupervised learning is used. The training model aids in the improvement of the training set’s probabilities and the maximal probability can be generated by looking at the weight assignment and it is shown in Eq. (31). Then, with respect to the energy function defined in Eq. (28), the assignment of the probability to every pair of visible and hidden neurons is done by RBM, which is expressed in Eq. (32). The energy of all the possible states is added up and this is known as the partition function that is expressed in Eq. (33).
| 31 |
| 32 |
| 33 |
Contrastive Divergence
It is a learning technique utilized for initializing the visible states and here the visible states need not be initialized randomly. Contrastive divergence (CD) initializes the visible states with the help of input data and further reconstructs the model expectations from the input data. The upcoming sections summarize the steps of the CD algorithm.
Training samples are chosen and they are braced against visible states.
- The hidden neuron’s probability is represented using the term and it is acquired via multiplying (visible vector) together with (weight matrix) as as per Eq. (34).
34 Then, from the acquired probability , the hidden states are sampled.
The positive gradient simply referred to as the outer product is computed by multiplying (visible vector) with (probability of hidden neurons) as per .
- Moreover, from (hidden vector), the reconstruction of visible states takes place, and then, the hidden states emerge from the reconstruction of (visible states).
35 The negative gradient simply referred to as the outer product is computed by multiplying and as per .
The computed positive gradient and negative gradient are subtracted to determine the weight updates as .
- Finally, the weights are changed using the new values.
For RBM, one of the renowned gradient approximations is CD. RBM and MLP layers are available in the architecture of DBN. Supervised learning is utilized in MLP and unsupervised learning in RBM.
Neural Network
NN intakes GLCM features and exhibits the presence or absence of brain tumors. NN is made up of three main layers: input, output, and hidden. Equations (36) and (37) express the NN network model numerically. The hidden layer has the hidden neurons , in which . The output neuron is in the output layer, in which . In addition, the input layer has input neurons , where . The bias weight of and is denoted as and , respectively. The weight from to and from to is represented as and . The error function is the difference between (actual outputs) and (predicted output). The overall features extracted from GLCM are and indicates the count of features. The notation in Eqs. (37) and (38) is the activation function. The mathematical formula for the hidden layer is depicted in Eq. (36).
| 36 |
| 37 |
| 38 |
Proposed Hybrid Algorithm for Hybrid Classifier Optimization: Objective Function and Solution Encoding
Objective Function
The primary goal of the current brain tumor segmentation study is to improve the classification’s accuracy and it is expressed in Eq. (39). As a result, a new hybrid method L-DSU will be used to maximize the hidden neurons of both classifiers (DBN and NN). Figure 2 shows the solution encoding for the suggested approach.
| 39 |
Fig. 2.
Solution encoding
Traditional Algorithms: LA and DA
LA [39]
It is a nature-inspired optimization algorithm which was inspired by the social behavior of lions, particularly territorial defense & conquest [40, 41]. The fundamental structure of LA encloses 6 key stages that are depicted in the upcoming section.
- Pride generation: This is the first step in the LA process, known as the initialization phase. Here, the male lion, female lion, and the nomad represented as , &, respectively are initialized. In addition, the vector element of , & are the random integers within the upper and the lower limits while and it is represented as , and , respectively, where and the term symbolizes the length of the lion that can be defined using Eq. (40). The notations and are the integers and they decide the value of ( lion length). Further, when , the search process continues with binary-encoded lion as well as this is ensured in the search space by Eq. (41).
40 41 -
Fertility evaluation: As days pass, the lions become old or become infertile and this makes the lions laggard in the terrestrial defense or terrestrial takeover. Further, in terms of fitness value,, have reached their global or local optimal. The fertility evaluation is used to prevent the solution from being trapped in the local optima. When , the male lion becomes laggard and the laggardness rate is enlarged via 1.
The reference fitness is symbolized as . The process of terrestrial defense occurs when . Moreover, the sterile rate confirms the fertility of as well as it is enlarged v 1 at the end of the crossover process. The updating of with occurs as per Eq. (42), while the mating process is performed. This process of updating continues, until reaches . Then, and vector elements of is &, respectively. In the interval resides the random integer . The female update function is represented as and the random integers generated within [0, 1] are represented as and . Mathematically, the female update function is shown in Eqs. (43) and (44), respectively.42 43 44 Mating: Here, two basic phases, crossover and mutation, as well as an additional step, gender clustering, are performed. The cubs are generated by , via undergoing crossover and mutation. During the generation of each cub, the cross-over mask is varied and hence is generated in mask. The cubs obtained from the crossover and mutation procedure are represented by , and are the cubs obtained through the crossover and mutation procedure. The obtained eight cubs fill the cub pool and produce and by gender clustering.
DA [42]
The inspiration for the method was derived from dragonfly swarming patterns, both static and dynamic. The exploitation and exploration phases of optimization are the most important, as they aid in replicating the social interaction between dragonflies while navigating, searching for food, and avoiding attackers. Attraction to the food source, detection from the enemy, separation, alignment, and control cohesion are the five key aspects of DA.
Separation: This is the process of separating dragonflies from neighboring individuals for avoiding static collision. Equation (50) shows the mathematical formula for separation. The location of the current swarm as well as its neighboring individual is denoted as , and the count of the neighbors of is symbolized as , respectively.
| 50 |
Alignment: The velocity of neighboring individuals is symbolized as and it is shown in Eq. (51).
| 51 |
Cohesion: Eq. (52) represents the numerical formula for cohesion.
| 52 |
Equation (53) shows the mathematical formula explaining the dragonflies’ attraction to the food source. The dragonfly’s distraction outwards while facing an attacker is mathematically demonstrated in Eq. (54)
| 53 |
| 54 |
The dragonflies’ position updates in the search space, and their movement is aided by two vectors: the step vector as well as the position vector . is the direction of the dragonflies’ movement which is mathematically stated in Eq. (55). Furthermore, the separation weight , alignment weight , cohesion weight , food factor , enemy factor , inertia weight , and current iteration along with the separation , alignment , cohesion , food source , and position of an enemy of individual together help to estimate . Following the computation of the step vector, the position vectors are computed using Eq. (55). In the absence of a nearby individual, dragonflies will use the random walk (Le’vy flight) to fly all over the search space. The dragonflies’ randomness, exploration, and stochastic behavior are all enhanced by this random walk. Equation (56) defines the position update with a random walk (Le’vy fly() levy), and the relevant limitations are discussed in Eqs. (57), (58) and (59), respectively. is the position vector dimension. The random numbers in the range [0, 1] are indicated by and and is a constant.
| 55 |
| 56 |
| 57 |
| 58 |
| 59 |
where .
L-DSU: Proposed Hybrid Algorithm
This research offers a new hybrid method, which coordinates the concepts of DA and LA to tackle the optimization issue in the suggested work, which obviously tends to eliminate the current shortcomings in traditional models. More particularly, even though the traditional DA is embedded with the potential of acquiring the global optimal solution, it suffers from less convergence rate. Similarly, the LA model also needs to be enhanced with respect to the convergence rate.
The proposed hybrid model combines the working principle of both the algorithms under certain means, which is described as follows: In conventional LA, the search agent s position is updated according to the female update given in Eq. (42). However, the proposed model makes changes in this update evaluation by evaluating the separation update of DA as in Eq. (50). As the DA update process is influenced by the LA update, the proposed model is referred to as the L-DSU model. Algorithm 1 displays the L-DSU pseudo-code, and Fig. 3 depicts the L-DSU flow chart.

Fig. 3.
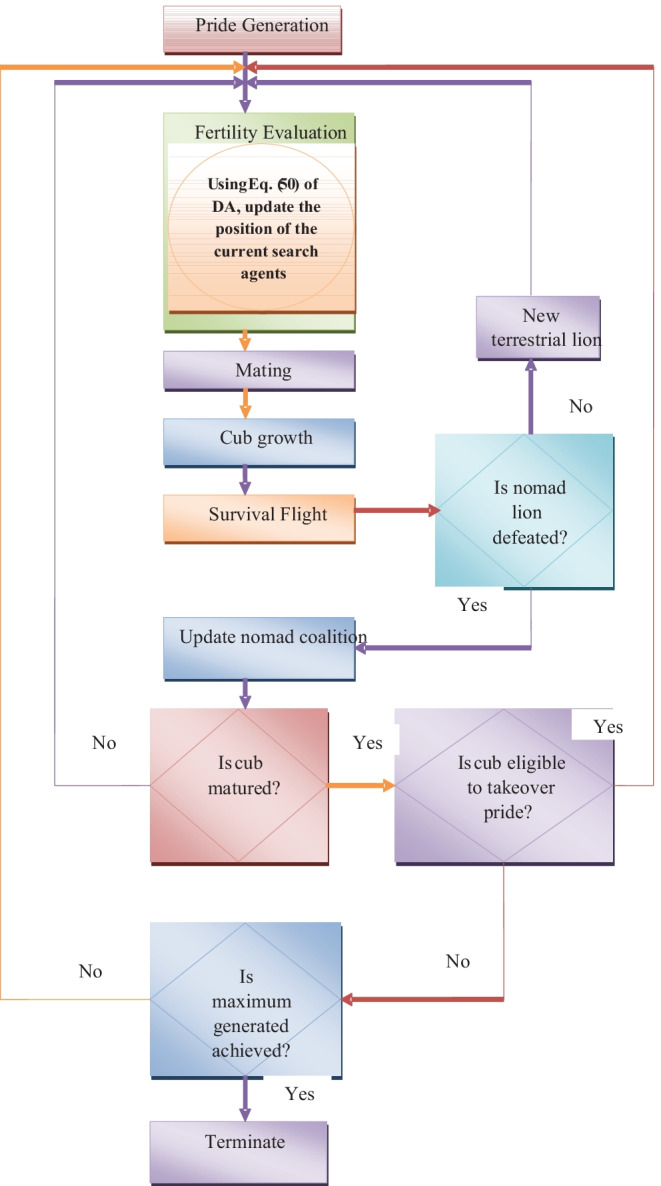
Flow chart of suggested L-DSU algorithm
Result and Discussion
Simulation Setting
The suggested L-DSU model is executed in MATLAB, and the results are examined using the dataset obtained from []. Table 3 provides a full description of dataset characteristics. Figure 4 shows some of the example photos from this dataset. Figure 4b depicts the filtered image, while Fig. 4c depicts the segmented image. Figure 5 illustrates the resultant images. In addition, Fig. 5b represents the output of skull scripting whereas Fig. 4c depicts the output of segmentation. Figure 6 depicts the comparison of segmentation results.
Table 3.
Dataset characteristics
| SI. no | Dataset characteristics |
|---|---|
| 1 | Total images = 3064 |
| 2 | Number of label = (1, 2, 3) |
| 3 | Label l1 = 708 |
| 4 | Label l2 = 1426 |
| 5 | Label l3 = 930 |
| 6 | Test case considered = 5 |
Fig. 4.
MRI image showing the a collected sample image, b filtered image, and c segmented image
Fig. 5.
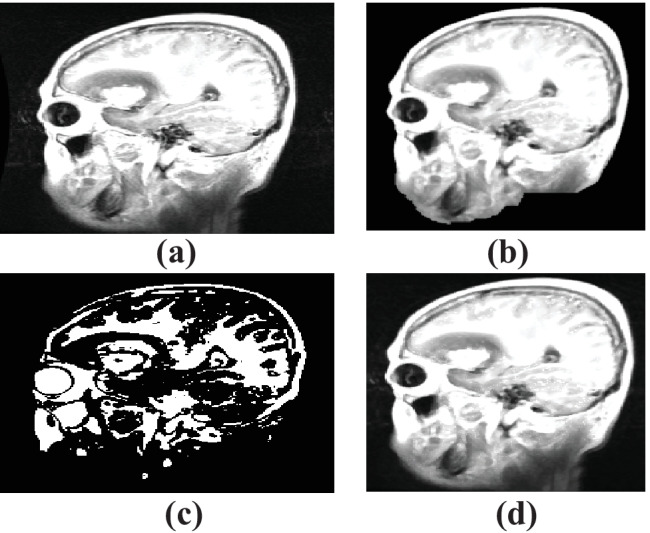
The output of the a original image, b skull scripting, c segmentation, and d entropy-based trilateral filter
Fig. 6.
Comparison of segmentation results of a FCM b K-means, and c adaptive CLFAH
The evaluation is carried out by partitioning the dataset into 5 test cases, namely test case 1, test case 2, test case 3, test case 4, and test case 5, correspondingly, to confirm the enhancement of the suggested brain tumor classification model over previous methods. In terms of the various measures, the performance of the suggested work was assessed by adjusting the Learning Percentage (LP) from 40 to 80%. This evaluation is done by having a comparison between the L-DSU and existing algorithms like PSO [44], FF [45], GWO [46], WOA [47], LA [39], LE-WOA [48], and DA [42], respectively. The classification performance of the proposed classifier and existing classifier is compared in addition with individual NN [49], DBN [38], RF-MPDAC [24], and MDCNN [26].
Evaluation on Performance of Proposed over Traditional Models for Test Case 1: Algorithmic and Classifier Evaluation
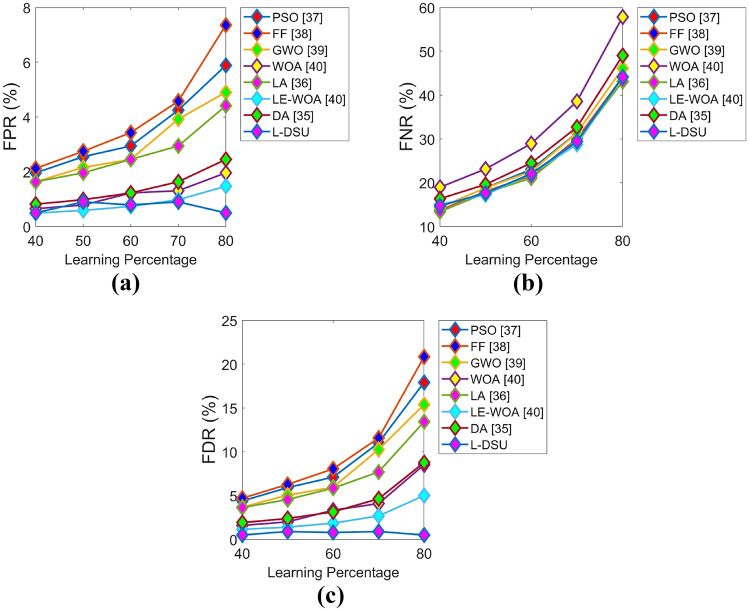
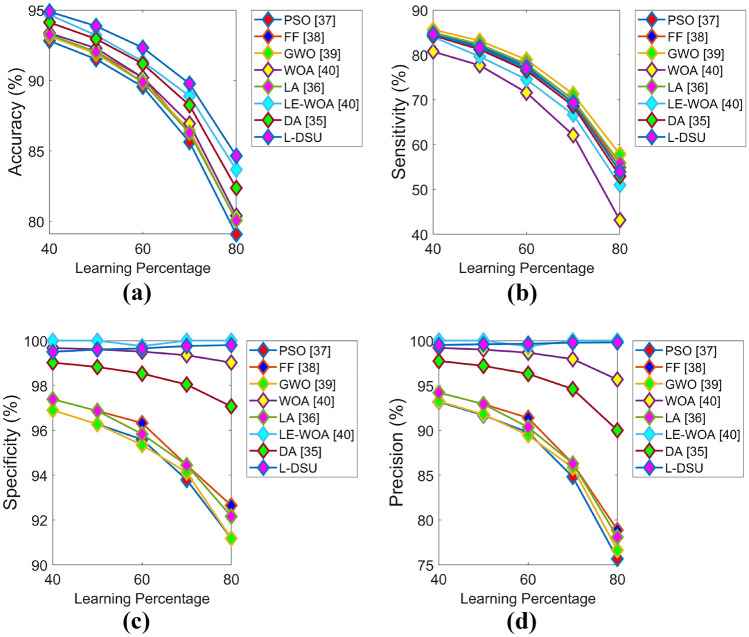
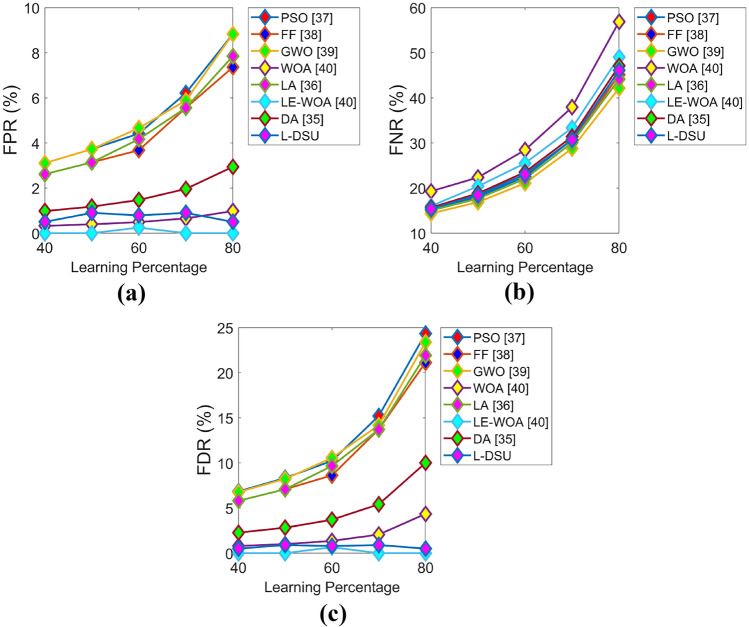
The positive and negative performance of the suggested study is performed for test case 1 with respect to algorithmic evaluation by varying LP and the resultant graphs are illustrated in Figs. 7 and 8. Since the classification accuracy with reduced errors plays a key role in this research (i.e., the objective), the accuracy of L-DSU in Fig. 7a at LP = 80% is 3.5%, 6.6%, 7.3%, 8.6%, 4.7%, 11.3%, and 6% greater than PSO, FF, GWO, WOA, LA, LE-WO, and DA, respectively. In the case of negative performance (error analysis), FPR of the L-DSU in Fig. 8a is 96%, 97.5%, 95.5%, 80%, 95%, 60%, and 86.6% greater than PSO, FF, GWO, WOA, LA, LE-WO, and DA, respectively.
Fig. 7.
Algorithmic evaluation of the L-DSU over the existing model for test case 1 shows positive measures of a accuracy, b sensitivity, c specificity, d precision
Fig. 8.
Algorithmic evaluation of the L-DSUover the existing model for test case 1 shows negative measures of a FPR, b FNR, and c FDR
Then, in the case of classifier evaluation in Table 4, the suggested hybrid classifier (DBN + NN) accuracy has achieved the highest value of 0.90196, which is 19.5% better than RF, CNN, and KNN, and 10.8% better than MLP. FNR of the suggested model has recorded the lowest value of 0.095238, which is 72.3% better than RF, 76.7% better than both KNN and CNN, and 79.3% better than MLP. The accuracy of the suggested hybrid classifier (DBN + NN) has reached a maximum value of 0.90196, as shown in Table 5 and the resultant is 10.8% and 11.5% better than MLP alone and DBN alone, respectively. As compared to the result of the literature, the proposed hybrid classifier (DBN + NN) accuracy is 11.1% and 11.5% higher than RF-MPDAC [24] and MDCNN [26] methodologies. All of the other positive measures except sensitivity are considerably greater when compared with RF-MPDAC [24] and MDCNN [26]. Thus, from the algorithmic as well as classifier-based evaluation, it is obvious that the L-DSU + NN + DBN is superior to the extant models in enhancing the classification accuracy.
Table 4.
Classifier analysis for test case 1
| Measures | RF [50] | KNN [51] | CNN [52] | NN [49] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.65574 | 0.67925 | 0.67925 | 0.97143 | 0.86364 |
| Specificity | 0.77174 | 0.81522 | 0.81522 | 0.98889 | 0.90000 |
| Accuracy | 0.72549 | 0.72549 | 0.72549 | 0.80392 | 0.90196 |
| F1-score | 0.65574 | 0.63158 | 0.63158 | 0.69388 | 0.88372 |
| Sensitivity | 0.65574 | 0.59016 | 0.59016 | 0.53968 | 0.90476 |
| MCC | 0.42748 | 0.41714 | 0.41714 | 0.61933 | 0.79970 |
| NPV | 0.77174 | 0.81522 | 0.81522 | 0.98889 | 0.90000 |
| FPR | 0.22826 | 0.18478 | 0.18478 | 0.01111 | 0.10000 |
| FDR | 0.34426 | 0.32075 | 0.32075 | 0.02857 | 0.13636 |
| FNR | 0.34426 | 0.40984 | 0.40984 | 0.46032 | 0.09523 |
Table 5.
Proposed hybrid versus individual classifiers: test case 1
| Measures | NN [49] | DBN [38] | RF-MPDAC [24] | MDCNN [26] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.97143 | 0.78571 | 0.68182 | 0.65934 | 0.86364 |
| Specificity | 0.98889 | 0.86667 | 0.69565 | 0.66304 | 0.90000 |
| Accuracy | 0.80392 | 0.79739 | 0.81046 | 0.79085 | 0.90196 |
| F1-score | 0.69388 | 0.73950 | 0.80537 | 0.78947 | 0.88372 |
| Sensitivity | 0.53968 | 0.69841 | 0.98361 | 0.98361 | 0.90476 |
| MCC | 0.61933 | 0.57733 | 0.67282 | 0.64493 | 0.79970 |
| NPV | 0.98889 | 0.86667 | 0.69565 | 0.66304 | 0.90000 |
| FPR | 0.01111 | 0.13333 | 0.30435 | 0.33696 | 0.10000 |
| FDR | 0.02857 | 0.21429 | 0.31818 | 0.34066 | 0.13636 |
| FNR | 0.46032 | 0.30159 | 0.01639 | 0.01639 | 0.09523 |
Evaluation on Performance of Proposed over Traditional Models for Test Case 2: Algorithmic and Classifier Evaluation
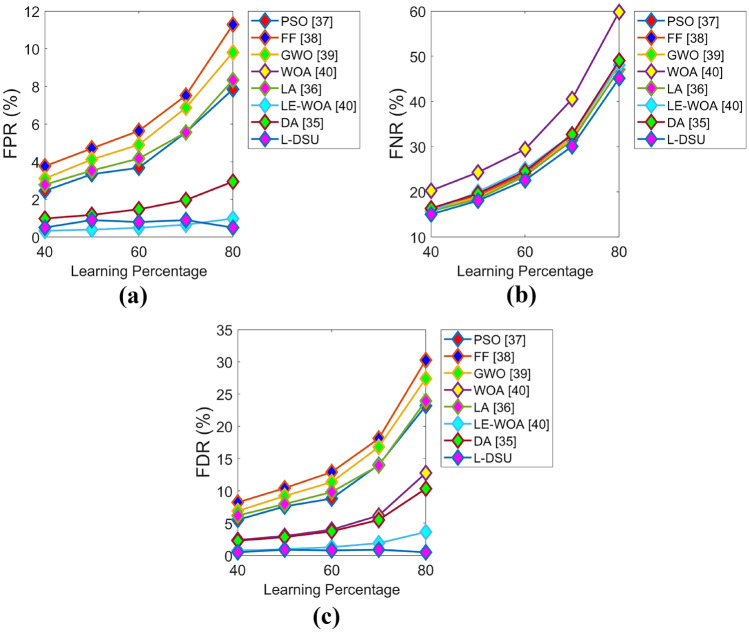
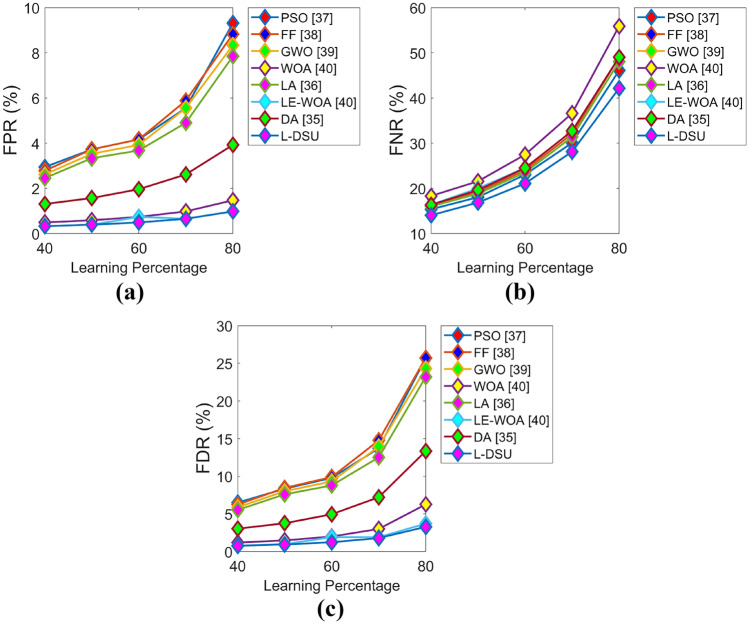
Figures 9 and 10 exhibit the algorithmic evaluation of the L-DSU by varying LP over the existing optimization model for test case 2 in terms of positive and negative performance, respectively. As shown in Fig. 9a, the L-DSU is 13.5%, 14.7%, 12.5%, 11.3%, 9%, 3.4%, and 6.8% more accurate than the conventional optimization algorithms like PSO, FF, GWO, WOA, LA, LE-WO, and DA at LP = 80%.
Fig. 9.
Algorithmic evaluation of the L-DSUover the conventional model for test case 2 for a accuracy, b sensitivity, c specificity, and d precision
Fig. 10.
Algorithmic evaluation of the L-DSUover the existing model for test case 2 for a FPR, b FNR, and c FDR
Table 6 compares the L-classifier DSU’s performance to that of traditional classifiers. Here, the maximum accuracy is achieved as 0.83007, which is 12.5%, 17.3%, 17.3%, and 7% better than RF, KNN, CNN, and MLP, respectively. The FDR of L-DSU with the lowest value (0.83007) is achieved by the proposed hybrid classifier (DBN + NN) and it is 50%, 53.6%, 53.6%, and 33.3% superior to RF, KNN, CNN, and MLP, respectively. Table 7 represents the classification performance of the suggested classifier over DBN alone and NN alone for Test case 2. Here, the highest accuracy is 0.83007 (in the proposed hybrid classifier (DBN + NN)), which is 7% and 10.2% better than DBN and NN, respectively, as well as the accuracy of the proposed hybrid classifier is 10.5% greater than RF-MPDAC [24] and MDCNN [26]. Thus, from the evaluation, it is vivid that the suggested hybrid classifier (DBN + NN) has enhanced performance over the existing one.
Table 6.
Classifier analysis for test case 2
| Measures | RF [50] | KNN [51] | CNN [52] | NN [49] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.64865 | 0.62121 | 0.62121 | 0.86842 | 0.82456 |
| Specificity | 0.70787 | 0.71910 | 0.71910 | 0.94444 | 0.88889 |
| Accuracy | 0.72549 | 0.68627 | 0.68627 | 0.77124 | 0.83007 |
| F1_score | 0.69565 | 0.63077 | 0.63077 | 0.65347 | 0.78333 |
| Sensitivity | 0.75000 | 0.64063 | 0.64063 | 0.52381 | 0.74603 |
| MCC | 0.45195 | 0.35828 | 0.35828 | 0.53337 | 0.64631 |
| NPV | 0.70787 | 0.71910 | 0.71910 | 0.94444 | 0.88889 |
| FPR | 0.29213 | 0.28090 | 0.28090 | 0.055556 | 0.11111 |
| FDR | 0.35135 | 0.37879 | 0.37879 | 0.13158 | 0.17544 |
| FNR | 0.25000 | 0.35938 | 0.35938 | 0.47619 | 0.25397 |
Table 7.
Performance analysis of proposed hybrid classifier for test case 2
| Measures | NN [49] | DBN [38] | RF-MPDAC [24] | MDCNN [26] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.86842 | 0.75000 | 0.60784 | 0.60194 | 0.82456 |
| Specificity | 0.94444 | 0.86667 | 0.56044 | 0.54945 | 0.88889 |
| Accuracy | 0.77124 | 0.74510 | 0.73856 | 0.73203 | 0.83007 |
| F1-score | 0.65347 | 0.64865 | 0.75610 | 0.75152 | 0.78333 |
| Sensitivity | 0.52381 | 0.57143 | 1.00000 | 1.00000 | 0.74603 |
| MCC | 0.53337 | 0.46467 | 0.58366 | 0.57510 | 0.64631 |
| NPV | 0.94444 | 0.86667 | 0.56044 | 0.54945 | 0.88889 |
| FPR | 0.05555 | 0.13333 | 0.43956 | 0.45055 | 0.11111 |
| FDR | 0.13158 | 0.25000 | 0.39216 | 0.39806 | 0.17544 |
| FNR | 0.47619 | 0.42857 | 0.00000 | 0.00000 | 0.25397 |
Evaluation on Performance of Proposed Over Traditional Models for Test Case 3: Algorithmic and Classifier Evaluation
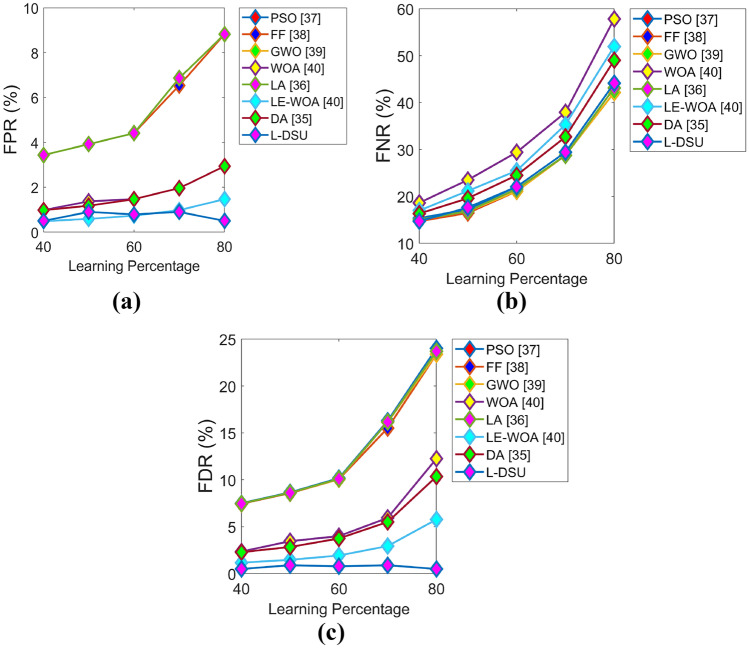
The optimization algorithm-based evaluation of the L-DSU over the traditional model on the basis of positive and negative measures for test case 3 by adjusting LP is visually displayed in Figs. 11 and 12. The L-DSU at LP = 40% has achieved the highest accuracy in Fig. 11a and it is 4.2%, 3.6%, 2.1%, 3.5%, 3.8%, 0.1%, and 3.1% better than optimization algorithms like PSO, FF, GWO, WOA, LA, LE-WO, and DA, respectively. Table 8 compares the classification performance of L-DSU + NN + DBN to classical classifiers for Test case 3. The highest accuracy (0.87582) is recorded by L-DSU + NN + D proposed hybrid classifier (DBN + NN) BN, which is 14.1%, 17.1%, 17.1%, and 2.23% superior to RF, KNN, CNN, and MLP, respectively. Then, in the case of classification performance of the proposed hybrid classifier (DBN + NN) over DBN alone and NN alone for test case 3 from Table 9, the L-DSU records the highest value as 0.87582 and the resultant is 2.2% and 9.7% enhanced over DBN alone and NN alone. The proposed method is 13.2% more accurate than the current method. MDCNN and RF-MPDAC, respectively. Of the resultants of all the three evaluations (algorithmic, classifier-based, and individual classifier performance-based evaluation), the proposed hybrid classifier (DBN + NN) exhibits higher performance, and hence, it is said to be much superior in performance.
Fig. 11.
Algorithmic evaluation of the L-DSUover the existing model for test case 3 for a accuracy, b sensitivity, c specificity, and d precision
Fig. 12.
Algorithmic evaluation of the L-DSUover the existing model for test case 3 for a FPR, b FNR, and c FDR
Table 8.
Classifier analysis for test case 3
| Measures | RF [50] | KNN [51] | CNN [52] | NN [49] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.65854 | 0.60976 | 0.60976 | 0.93103 | 0.74138 |
| Specificity | 0.86275 | 0.84314 | 0.84314 | 0.98113 | 0.85849 |
| Accuracy | 0.75163 | 0.72549 | 0.72549 | 0.85621 | 0.87582 |
| F1-score | 0.58696 | 0.54348 | 0.54348 | 0.71053 | 0.81905 |
| Sensitivity | 0.52941 | 0.49020 | 0.49020 | 0.57447 | 0.91489 |
| MCC | 0.41739 | 0.35478 | 0.35478 | 0.65396 | 0.73540 |
| NPV | 0.86275 | 0.84314 | 0.84314 | 0.98113 | 0.85849 |
| FPR | 0.13725 | 0.15686 | 0.15686 | 0.01886 | 0.14151 |
| FDR | 0.34146 | 0.39024 | 0.39024 | 0.06896 | 0.25862 |
| FNR | 0.47059 | 0.50980 | 0.50980 | 0.42553 | 0.08510 |
Table 9.
Analysis of performance of the suggested hybrid classifier for test case 3
| Measures | NN [49] | DBN [38] | RF-MPDAC [24] | MDCNN [26] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.93103 | 0.63158 | 0.58586 | 0.58000 | 0.74138 |
| Specificity | 0.98113 | 0.80189 | 0.56842 | 0.55789 | 0.85849 |
| Accuracy | 0.85621 | 0.79085 | 0.73203 | 0.72549 | 0.87582 |
| F1_score | 0.71053 | 0.69231 | 0.73885 | 0.73418 | 0.81905 |
| Sensitivity | 0.57447 | 0.76596 | 1.00000 | 1.00000 | 0.91489 |
| MCC | 0.65396 | 0.54182 | 0.57707 | 0.56884 | 0.73540 |
| NPV | 0.98113 | 0.80189 | 0.56842 | 0.55789 | 0.85849 |
| FPR | 0.01886 | 0.19811 | 0.43158 | 0.44211 | 0.14151 |
| FDR | 0.06896 | 0.36842 | 0.41414 | 0.42000 | 0.25862 |
| FNR | 0.42553 | 0.23404 | 0.00000 | 0.00000 | 0.08510 |
Evaluation on Performance of Proposed Over Traditional Models for Test Case 4: Algorithmic and Classifier Evaluation
The L-DSU is compared on the basis of positive and negative measures over the existing optimization model by varying LP for test case 4 is manifested in Figs. 13 and 14, respectively. Initially, at LP = 80% in Fig. 13a, the accuracy of the L-DSU is 8.6%, 6%, 6.4%, 7.2%, 7.5%, 3.2, and 4.3% higher than the traditional approaches such as PSO, FF, GWO, WOA, LA, LE-WO, and DA, respectively. In the case of classification performance for test case 4, the proposed hybrid classifier (DBN + NN) achieves the maximum accuracy of 0.90196, which is 18.8%, 13.7%, 13.7%, and 2.17% greater than RF, KNN, CNN, and MLP, respectively, from Table 10. Further, the proposed hybrid classifier (DBN + NN) in the case of individual classifier analysis in Table 11 shows an enhancement of 2.1% and 11.59% over MLP alone and DBN alone and 14.56% and 15.27% over RF-MPDAC and MDCNN approach in terms of accuracy (highest value by proposed = 0.90196. As a result, under the three assessments for test case 4, the suggested hybrid classifier (DBN + NN) outperforms the traditional one.
Fig. 13.
Algorithmic evaluation of the L-DSUover the traditional model for test case 4 for a accuracy, b sensitivity, c specificity, and d precision
Fig. 14.
Algorithmic evaluation of the L-DSUover the existing model for test case 4 for a FPR, b FNR, and c FDR
Table 10.
Classifier analysis for test case 4
| Measures | RF [50] | KNN [51] | CNN [52] | NN [49] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.58025 | 0.72727 | 0.72727 | 0.97222 | 0.82456 |
| Specificity | 0.65657 | 0.87879 | 0.87879 | 0.99010 | 0.90099 |
| Accuracy | 0.73203 | 0.77778 | 0.77778 | 0.88235 | 0.90196 |
| F1_score | 0.69630 | 0.65306 | 0.65306 | 0.79545 | 0.86239 |
| Sensitivity | 0.87037 | 0.59259 | 0.59259 | 0.67308 | 0.90385 |
| NPV | 0.65657 | 0.87879 | 0.87879 | 0.99010 | 0.90099 |
| MCC | 0.50450 | 0.49768 | 0.49768 | 0.74054 | 0.78849 |
| FPR | 0.34343 | 0.12121 | 0.12121 | 0.00990 | 0.09901 |
| FDR | 0.41975 | 0.27273 | 0.27273 | 0.02777 | 0.17544 |
| FNR | 0.12963 | 0.40741 | 0.40741 | 0.32692 | 0.09615 |
Table 11.
Analysis of performance of the suggested hybrid classifier for test case 4
| Measures | NN [49] | DBN [38] | RF-MPDAC [24] | MDCNN [26] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.97222 | 0.71429 | 0.56471 | 0.54545 | 0.82456 |
| Specificity | 0.99010 | 0.86139 | 0.64762 | 0.61905 | 0.90099 |
| Accuracy | 0.88235 | 0.79739 | 0.75817 | 0.73856 | 0.90196 |
| F1-score | 0.79545 | 0.69307 | 0.72180 | 0.70588 | 0.86239 |
| Sensitivity | 0.67308 | 0.67308 | 1.00000 | 1.00000 | 0.90385 |
| MCC | 0.74054 | 0.54258 | 0.60474 | 0.58109 | 0.78849 |
| NPV | 0.99010 | 0.86139 | 0.64762 | 0.61905 | 0.90099 |
| FPR | 0.00990 | 0.13861 | 0.35238 | 0.38095 | 0.09901 |
| FDR | 0.02777 | 0.28571 | 0.43529 | 0.45455 | 0.17544 |
| FNR | 0.32692 | 0.32692 | 0.00000 | 0.00000 | 0.09615 |
Evaluation on Performance of Proposed Over Traditional Models for Test Case 5: Algorithmic and Classifier Evaluation
Figures 15 and 16 demonstrate the optimization algorithm-based performance evaluation in terms of positive and negative measures for test case 5 by adjusting LP. The accuracy of the L-DSU is higher in Fig. 15a and the resultant is 4.2%, 3.6%, 2.1%, 3.15%, 2.6%, 1.05%, & 1.26% higher than PSO, FF, GWO, WOA, LA, LE-WO, and DA, respectively, at LP = 80%. Further, in the case of classifier-based evaluation in Table 12, the highest classification accuracy is recorded by the proposed hybrid classifier (DBN + NN) as 0.87582, which is 8.2% greater than RF, 14.1% better than both KNN and CNN, and 4.4% higher than MLP, respectively. Figures 15 and 16 demonstrate the optimization algorithm-based performance evaluation in terms of positive and negative measures for test case 5 by adjusting LP in addition it is 4.4% and 10.4% superior to NN and DBN, and 12.34% and 15.43% higher to RF-MPDAC and MDCNN respectively. The evaluation of the L-DSU for test case 5 exhibited higher values in the case of positive measures and lower values in the case of certain negative measures and hence verified the supremacy of L-DSU. In addition, the convergence graph in Fig. 17 is used to evaluate the correction between PSO, FF, GWO, WOA, LA, RF-MPDAC, and L-DSU. The performance analysis of the suggested hybrid classifier for test case 5 is shown in Table 13.
Fig. 15.
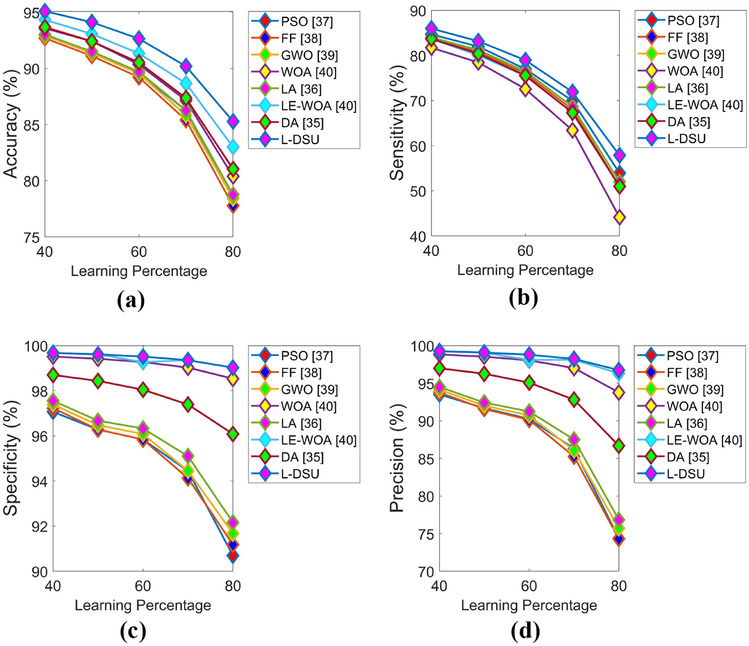
Algorithmic evaluation of the L-DSUover the traditional model for test case 5 for a accuracy, b sensitivity, c specificity, and d precision
Fig. 16.
Algorithmic evaluation of the L-DSUover the existing model for test case 5 for a FPR, b FNR, and c FDR
Table 12.
Classifier analysis for test case 5
| Measures | RF [50] | KNN [51] | CNN [52] | NN [49] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.80952 | 0.78182 | 0.78182 | 0.97059 | 0.79688 |
| Specificity | 0.85714 | 0.85714 | 0.85714 | 0.98958 | 0.86458 |
| Accuracy | 0.80392 | 0.75163 | 0.75163 | 0.83660 | 0.87582 |
| F1_score | 0.77273 | 0.69355 | 0.69355 | 0.72527 | 0.84298 |
| Sensitivity | 0.73913 | 0.62319 | 0.62319 | 0.57895 | 0.89474 |
| MCC | 0.60286 | 0.49809 | 0.49809 | 0.66117 | 0.74424 |
| NPV | 0.85714 | 0.85714 | 0.85714 | 0.98958 | 0.86458 |
| FPR | 0.14286 | 0.14286 | 0.14286 | 0.01041 | 0.13542 |
| FDR | 0.19048 | 0.21818 | 0.21818 | 0.02941 | 0.20313 |
| FNR | 0.26087 | 0.37681 | 0.37681 | 0.42105 | 0.10526 |
Fig. 17.
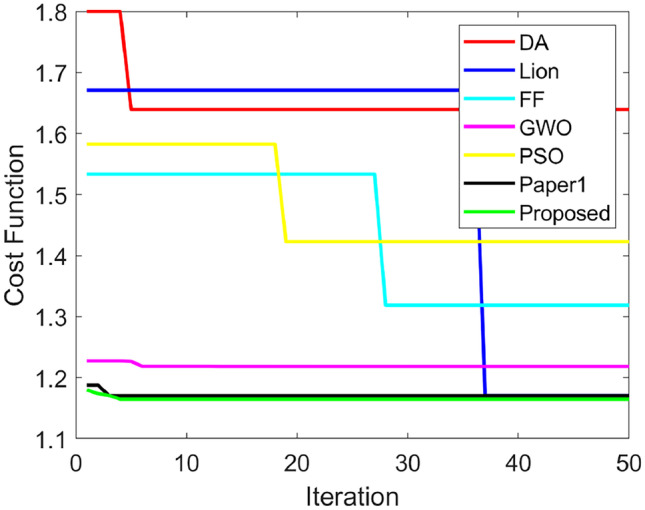
Convergence graph
Table 13.
Analysis of performance of the suggested hybrid classifier for test case 5
| Measures | NN [49] | DBN [38] | RF-MPDAC [24] | MDCNN [26] | Proposed hybrid classifier (NN + DBN) |
|---|---|---|---|---|---|
| Precision | 0.97059 | 0.72222 | 0.60000 | 0.57447 | 0.79688 |
| Specificity | 0.98958 | 0.84375 | 0.63636 | 0.59596 | 0.86458 |
| Accuracy | 0.83660 | 0.78431 | 0.76471 | 0.73856 | 0.87582 |
| F1_score | 0.72520 | 0.70270 | 0.75000 | 0.72973 | 0.84298 |
| Sensitivity | 0.57895 | 0.68421 | 1.00000 | 1.00000 | 0.89474 |
| MCC | 0.66110 | 0.53415 | 0.61791 | 0.58512 | 0.74424 |
| NPV | 0.98958 | 0.84375 | 0.63636 | 0.59596 | 0.86458 |
| FPR | 0.01041 | 0.15625 | 0.36364 | 0.40404 | 0.13542 |
| FDR | 0.02941 | 0.27778 | 0.40000 | 0.42553 | 0.20313 |
| FNR | 0.42105 | 0.31579 | 0.00000 | 0.00000 | 0.10526 |
Analysis of Segmentation Results
The segmentation results of the Jaccard and Dice coefficient for the proposed adaptive CLFAHE and traditional methods are depicted in Table 14. On analyzing the results, it can be noticed that the suggested model attains a higher value for the Jaccard coefficient, that is, the proposed model is 42.29% and 29.31% better than the conventional K-means as well as fuzzy C-means. Likewise, for the Dice coefficient, the adopted method is 51.58% and 34.79% superior to K-means and fuzzy C-means segmentation, respectively.
Table 14.
Analysis of segmented results for proposed adaptive CLFAHE and traditional methods
| Methods | Jaccard | Dice |
|---|---|---|
| Adaptive CLFAHE | 0.70608 | 0.82773 |
| K-means | 0.40035 | 0.40071 |
| Fuzzy C-means | 0.52026 | 0.53971 |
Conclusion
When it comes to making diagnostic judgments for patients, medical software is a critical factor to consider. This paper introduces an improvement to the brain tumor categorization paradigm. The novel hybrid method can be utilized to determine brain cancers at an early stage in real-time applications. The current research paper has expanded a novel brain tumor classification model via following six major steps as follows, denoising, skull stripping, segmentation, feature extraction, and classification. Initially, the entropy-based trilateral filter was used to de-noise the collected brain tumor MRI picture. The de-noised image was subjected to skull stripping via Otsu thresholding as well as morphological segmentation. Subsequently, the de-noised image was segmented using CLFAHE. Then, from the segmented image, the GLCM features were retrieved, then these mined GLCM features were classified using DBN and NN. The detection accuracy of brain tumors was improved by using the newly created L-DSU technique to optimize the hidden neurons of both the classifiers (DBN and NN). Finally, the proposed L-DSU model’s performance was compared to that of standard approaches in terms of algorithmic and classification-based evaluation. The accuracy of the L-DSU is higher in Test case 5 and the resultant is 4.2%, 3.6%, 2.1%, 3.15%, 2.6%, 1.05%, and 1.26% higher than PSO, FF, GWO, WOA, LA, LE-WO, and DA, respectively, at LP = 80%. In case of negative performance, the FPR of the L-DSU for Test case 1 is 96%, 97.5%, 95.5%, 80%, 95%, 60%, and 86.6% superior to PSO, FF, GWO, WOA, LA, LE-WO, and DA, respectively. In the case of classification performance for test case 4, the proposed hybrid classifier (DBN + NN) achieves the maximum accuracy of 0.90196, which is 18.8%, 13.7%, 13.7%, and 2.17% better than RF, KNN, CNN, and MLP, respectively. The suggested model has limitations in that it has not been tested on volumes with more than one tumor per slice. In the future study, the parallel segmentation approach will be employed to reduce the complexity of the suggested model even more. Future work could involve expanding the suggested model to deal with other regions of tumors and examining the influence of level set segmentation and the dragonfly algorithm variables on the model’s accuracy.
Abbreviations
- ANN
Artificial neural network
- BPN
Back propagation neural
- CLFAHE
Contrast limited fuzzy adaptive histogram equalization
- CT
Computer tomography
- DA
Dragonfly algorithm
- DBN
Deep belief network
- ERT
Extremely randomized tree
- FDR
False discovery rate
- FNR
False-negative rate
- FPR
False-positive rate
- GA
Genetic algorithm
- GLDM
Gray-level difference matrix
- KNN
K-nearest neighbor
- LA
Lion algorithm
- L-DSU
Lion with dragonfly separation update
- LE-WOA
Lion exploration-based whale optimization
- MCC
Matthews correlation coefficient
- MDCNN
Modified deep convolutional neural network
- MRI
Magnetic resonance imaging
- NN
Neural network
- NPV
Negative predictive value
- RFCM
Rough-fuzzy C-means
- RF-MPDAC
Random forests with multiscale patch-driven active contour
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Huang M, Yang W, Wu Y, Jiang J, Chen W, Feng Q. Brain Tumor Segmentation Based on Local Independent Projection-Based Classification. IEEE Transactions on Biomedical Engineering. 2014;61(10):2633–2645. doi: 10.1109/TBME.2014.2325410. [DOI] [PubMed] [Google Scholar]
- 2.Sallemi L, Njeh I, Lehericy S. Towards a Computer Aided Prognosis for Brain Glioblastomas Tumor Growth Estimation. IEEE Transactions on NanoBioscience. 2015;14(7):727–733. doi: 10.1109/TNB.2015.2450365. [DOI] [PubMed] [Google Scholar]
- 3.Demirhan A, Törü M, Güler I. Segmentation of Tumor and Edema Along With Healthy Tissues of Brain Using Wavelets and Neural Networks. IEEE Journal of Biomedical and Health Informatics. 2015;19(4):1451–1458. doi: 10.1109/JBHI.2014.2360515. [DOI] [PubMed] [Google Scholar]
- 4.M. G. Kounelakis et al., Strengths and weaknesses of 1.5T and 3T MRS data in brain glioma classification. IEEE Transactions on Information Technology in Biomedicine, vol. 15, no. 4, pp. 647–654, July 2011. [DOI] [PubMed]
- 5.Sun K, Pheiffer TS, Simpson AL, Weis JA, Thompson RC, Miga MI. Near Real-Time Computer Assisted Surgery for Brain Shift Correction Using Biomechanical Models. IEEE Journal of Translational Engineering in Health and Medicine. 2014;2:1–13. doi: 10.1109/JTEHM.2014.2327628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Braile, A., Toro, G., De Cicco, A., Cecere, A .B., Zanchini, F. and Panni, A .S., (2021). Hallux rigidus treated with adipose-derived mesenchymal stem cells: A case report. World Journal of Orthopedics. vol. 12, no. 1, p.51. [DOI] [PMC free article] [PubMed]
- 7.Nekrasov S, Zhyhylii D, Dovhopolov A, Karatas MA. Research on the manufacture and strength of the innovative joint of FRP machine parts. Journal of Manufacturing Processes. 2021;72:338–349. doi: 10.1016/j.jmapro.2021.10.025. [DOI] [Google Scholar]
- 8.Huda S, Yearwood J, Jelinek HF, Hassan MM, Fortino G, Buckland M. A Hybrid Feature Selection With Ensemble Classification for Imbalanced Healthcare Data: A Case Study for Brain Tumor Diagnosis. IEEE Access. 2016;4:9145–9154. doi: 10.1109/ACCESS.2016.2647238. [DOI] [Google Scholar]
- 9.Wu G, et al. Sparse Representation-Based Radiomics for the Diagnosis of Brain Tumors. IEEE Transactions on Medical Imaging. 2018;37(4):893–905. doi: 10.1109/TMI.2017.2776967. [DOI] [PubMed] [Google Scholar]
- 10.Z. Nie et al., Integrated time-resolved fluorescence and diffuse reflectance spectroscopy instrument for intraoperative detection of brain tumor margin. IEEE Journal of Selected Topics in Quantum Electronics, vol. 22, no. 3, pp. 49–57, May-June 2016.
- 11.Su H, Xing F, Yang L. Robust Cell Detection of Histopathological Brain Tumor Images Using Sparse Reconstruction and Adaptive Dictionary Selection. IEEE Transactions on Medical Imaging. 2016;35(6):1575–1586. doi: 10.1109/TMI.2016.2520502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Giordano C, Monica I, Quattrini F, Villaggi E, Gobbi R, Barbattini L. Evaluation Of The Radiation Dose To The Hands Of Orthopaedic Surgeons During Fluoroscopy Using Stored Images. Radiat Prot Dosimetry. 2020;189(2):157–162. doi: 10.1093/rpd/ncaa026. [DOI] [PubMed] [Google Scholar]
- 13.Maniscalco P, Quattrini F, Ciatti C, Gattoni S, Puma Pagliarello C, Burgio V, Di Stefano G, Cauteruccio M, Giovanelli M, Magro A, Capelli P, The Italian Covid-19 Phase 2 in Piacenza: results of the first semester of 2020 and future prospective of new orthopedics surgical procedures. Acta Biomed. 2020 Nov 10; 91(4):e2020159. 10.23750/abm.v91i4.10377. PMID: 33525208; PMCID: PMC7927514. [DOI] [PMC free article] [PubMed]
- 14.P. M. Shakeel, T. E. E. Tobely, H. Al-Feel, G. Manogaran and S. Baskar, Neural network based brain tumor detection using wireless infrared imaging sensor. IEEE Access, vol. 7, pp. 5577–5588, 2019.
- 15.N. Alan, A. Seicean, S. Seicean, D. Neuhauser, E. C. Benzel, and R. J. Wei, Preoperative steroid use and the incidence of perioperative complications in patients undergoing craniotomy for definitive resection of a malignant brain tumor. Journal of Clinical Neuroscience, vol. 22, no. 9, pp. 1413–1419, September 2015. [DOI] [PubMed]
- 16.Arnaud A, Forbes F, Coquery N, Collomb N, Lemasson B, Barbier EL. Fully Automatic Lesion Localization and Characterization: Application to Brain Tumors Using Multiparametric Quantitative MRI Data. IEEE Transactions on Medical Imaging. 2018;37(7):1678–1689. doi: 10.1109/TMI.2018.2794918. [DOI] [PubMed] [Google Scholar]
- 17.S. Shen, W. Sandham, M. Granat and A. Sterr, MRI fuzzy segmentation of brain tissue using neighborhood attraction with neural-network optimization. IEEE Transactions on Information Technology in Biomedicine, vol. 9, no. 3, pp. 459–467, Sept. 2005. [DOI] [PubMed]
- 18.Chen X, Nguyen BP, Chui C, Ong S. Reworking Multilabel Brain Tumor Segmentation: An Automated Framework Using Structured Kernel Sparse Representation. IEEE Systems, Man, and Cybernetics Magazine. 2017;3(2):18–22. doi: 10.1109/MSMC.2017.2664158. [DOI] [Google Scholar]
- 19.B. Anderson, Previously undiagnosed malignant brain tumor discovered during examination of a patient seeking chiropractic care. Journal of Chiropractic Medicine, vol. 15, no. 1, pp. 42–46, March 2016. [DOI] [PMC free article] [PubMed]
- 20.Bauer S, May C, Dionysiou D, Stamatakos G, Buchler P, Reyes M. Multiscale Modeling for Image Analysis of Brain Tumor Studies. IEEE Transactions on Biomedical Engineering. 2012;59(1):25–29. doi: 10.1109/TBME.2011.2163406. [DOI] [PubMed] [Google Scholar]
- 21.B. Song, P. Wen, T. Ahfock and Y. Li, Numeric investigation of brain tumor influence on the current distributions during transcranial direct current stimulation. IEEE Transactions on Biomedical Engineering, vol. 63, no. 1, pp. 176–187, Jan. 2016. [DOI] [PubMed]
- 22.Nguyen NX, Tran K, Nguyen TA. Impact of Service Quality on In-Patients’ Satisfaction, Perceived Value, and Customer Loyalty: A Mixed-Methods Study from a Developing Country. Patient preference and adherence. 2021;15:2523. doi: 10.2147/PPA.S333586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tran K, Nguyen T. Preliminary Research on the Social Attitudes toward the AI’s Involved Christian Education in Vietnam: Promoting AI Technology for Religious Education. Religions. 2021;12(3):208. doi: 10.3390/rel12030208. [DOI] [Google Scholar]
- 24.Ma C, Luo G, Wang K. Concatenated and Connected Random Forests With Multiscale Patch Driven Active Contour Model for Automated Brain Tumor Segmentation of MR Images. IEEE Transactions on Medical Imaging. 2018;37(8):1943–1954. doi: 10.1109/TMI.2018.2805821. [DOI] [PubMed] [Google Scholar]
- 25.V. Anitha and S. Murugavalli, Brain tumour classification using two-tier classifier with adaptive segmentation technique. In IET Computer Vision, vol. 10, no. 1, pp. 9–17, 2 2016.
- 26.D. J. Hemanth, J. Anitha, A. Naaji, O. Geman, D. E. Popescu and L. Hoang Son, A modified deep convolutional neural network for abnormal brain image classification. IEEE Access, vol. 7, pp. 4275–4283, 2019.
- 27.D. J. Hemanth, and J. Anitha, Modified genetic algorithm approaches for classification of abnormal magnetic resonance brain tumour images. Applied Soft Computing, Vol. 75, pp. 21–28, February 2019.
- 28.Z. U. Rehman, S. S. Naqvi, T. M. Khan, M. A. Khan, and T. Bashir, Fully automated multi-parametric brain tumour segmentation using superpixel based classification. Expert Systems with Applications, Vol. 118, pp. 598–613, March 2019.
- 29.Chen S, Ding C, Liu M. Dual-force convolutional neural networks for accurate brain tumor segmentation. Pattern Recognition. 2019;88:90–100. doi: 10.1016/j.patcog.2018.11.009. [DOI] [Google Scholar]
- 30.A. Bal, M. Banerjee, A. Chakrabarti, and P. Sharma, MRI brain tumor segmentation and analysis using rough-fuzzy C-means and shape based properties. Journal of King Saud University - Computer and Information Sciences, November 2018.
- 31.A. Pinto, S. Pereira, D. Rasteiro, and C. A. Silva, Hierarchical brain tumour segmentation using extremely randomized trees. Pattern Recognition, Vol. 82, pp. 105–117, October 2018.
- 32.Chang H. Entropy-based trilateral filtering for noise removal in digital images. 2010 3rd International Congress on Image and Signal Processing, Yantai. 2010;1:673–677. doi: 10.1109/CISP.2010.5647219. [DOI] [Google Scholar]
- 33.J. Yousefi, Image binarization using otsu thresholding algorithm. 2015.
- 34.R. Srisha, and A. M. Khan, Morphological operations for image processing. Understanding and its Applications, 2013.
- 35.M. Asha, and M. K. Gupta, A basic approach to enhance a gray scale image. Imperial Journal of Interdisciplinary Research (IJIR), vol. 2, no. 7, 2016.
- 36.EbeyHoneycutt Chris. RoyPlotnick,"Image analysis techniques and gray-level co-occurrence matrices (GLCM) for calculating bioturbation indices and characterizing biogenic sedimentary structures". Computers & Geosciences. 2008;34(11):1461–1472. doi: 10.1016/j.cageo.2008.01.006. [DOI] [Google Scholar]
- 37.Tang Binbin, Liu Xiao, Lei Jie, Song Mingli, Dong Fangmin. DeepChart: Combining deep convolutional networks and deep belief networks in chart classification. Signal Processing. 2016;124:156–161. doi: 10.1016/j.sigpro.2015.09.027. [DOI] [Google Scholar]
- 38.K. Mannepalli, P. N. Sastry and M. Suman, A novel Adaptive Fractional Deep Belief Networks for speaker emotion recognition. Alexandria Engineering Journal, October 2016.
- 39.Boothalingam Rajakumar. Optimization using lion algorithm: a biological inspiration from lion’s social behavior. Evolutionary Intelligence. 2018;11(1–2):31–52. doi: 10.1007/s12065-018-0168-y. [DOI] [Google Scholar]
- 40.B. R. Rajakumar, Lion algorithm for standard and large scale bilinear system identification: A global optimization based on Lion's social behavior. 2014 IEEE Congress on Evolutionary Computation, Beijing, China, pages: 2116–2123, July 2014.
- 41.B. R. Rajakumar, The lion's algorithm: a new nature inspired search algorithm. Procedia Technology-2nd International Conference on Communication, Computing & Security, Vol. 6, pages: 126–135, 2012
- 42.S. Mirjalili, Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Computing and Applications, vol. 27, no. 4, pp 1053–1073, May 2016.
- 44.Pedersen MEH, Chipperfield AJ. Simplifying Particle Swarm Optimization. Applied Soft Computing. 2010;10(2):618–628. doi: 10.1016/j.asoc.2009.08.029. [DOI] [Google Scholar]
- 45.Gandomi AH, Yang X-S, Talatahari S, Alavi AH. Firefly algorithm with chaos. Commun Nonlinear Sci Numer Simulat. 2013;18:89–98. doi: 10.1016/j.cnsns.2012.06.009. [DOI] [Google Scholar]
- 46.Mirjalili Seyedali. Seyed Mohammad Mirjalili, Andrew Lewis, "Grey Wolf Optimizer". Advances in Engineering Software. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
- 47.Mirjalili Seyedali. Andrew Lewisa,"The Whale Optimization Algorithm". Advances in Engineering Software. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- 48.B. Leena, Brain tumor segmentation and classification via adaptive CLFAHE with hybrid classification. In Communication, 2019.
- 49.F. Özyurt, E. Sert, and D. Avcı, An expert system for brain tumor detection: Fuzzy C-means with super resolution and convolutional neural network with extreme learning machine. Medical Hypotheses, Vol. 134, January 2020. [DOI] [PubMed]
- 50.Yang Tiejun, Song Jikun. Lei Li,"A deep learning model integrating SK-TPCNN and random forests for brain tumor segmentation in MRI". Biocybernetics and Biomedical Engineering. 2019;39(3):613–623. doi: 10.1016/j.bbe.2019.06.003. [DOI] [Google Scholar]
- 51.Comelli Albert, Stefano Alessandro, Russo Giorgio, Bignardi Samuel. Anthony Yezzi,"K-nearest neighbor driving active contours to delineate biological tumor volumes". Engineering Applications of Artificial Intelligence. 2019;81:133–144. doi: 10.1016/j.engappai.2019.02.005. [DOI] [Google Scholar]
- 52.Sajjad Muhammad, Khan Salman, Muhammad Khan, Wanqing Wu. Sung Wook Baik,"Multi-grade brain tumor classification using deep CNN with extensive data augmentation". Journal of Computational Science. 2019;30:174–182. doi: 10.1016/j.jocs.2018.12.003. [DOI] [Google Scholar]