Квадратура на кръга
Квадратурата на кръга е една от трите знаменити нерешими задачи на древността, занимавали умовете на математиците с векове.
Нейната формулировка е следната:
Да се начертае с помощта на линийка и пергел квадрат, равнолицев с даден кръг.
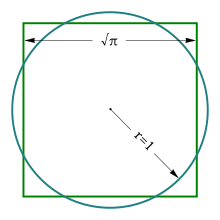
Задачата за квадратурата на кръга е тясно свързана с числото π. Наистина нека е дадена окръжност с радиус r. Лицето на заградения от нея кръг е равно на числото π r2. Ако дължината на страната на квадрат, равнолицев с този кръг, е x, то е в сила равенството x2 = π r2, откъдето следва .
Следователно квадратурата на кръга би била възможна само с линийка и пергел, ако с тези инструменти е построима отсечка с дължина . Когато отсечката r е избрана за единична, построима трябва да бъде отсечката с дължина . Последното предположение е равносилно с допускането за елементарна построимост на отсечка с дължина π при дадена единична отсечка.
Както знаем, отсечка с дължина π би била построима само с линийка и пергел, ако числото π е алгебрично и удовлетворява неразложимо алгебрично уравнение с цели коефициенти, чиято степен е от вида 2n (n – естествено число). И след многовековни математически усилия през 1882 г. Фердинанд Линдеман доказва, че π не е алгебрично, а трансцендентно число. Поради това то не е построимо и задачата за квадратурата на кръга е нерешима.
История
[редактиране | редактиране на кода]Още в най-стари времена са били известни методи за пресмятане на лице на кръг. В 50-ата задача в папируса на Райнд (около 1650 пр.н.е.) като лице на кръг с диаметър 9 е даден квадрат със страна 8, което отговаря на стойност на числото π = 3 13/81 = 3,16... Такива решения са били нещо обикновено за практиката. Още повече, че тогава много не са правели разлика между точно и приближено решение.
Задачата за квадратурата на кръга възниква не по-късно от V век пр.н.е. По това време вече са известни някои точни формули за лицето на триъгълника. Лицата на многоъгълниците били пресмятани посредством разлагането им на триъгълници. Построяването на квадрат – само с линийка и пергел, който да бъде равнолицев на даден триъгълник, било лесна задача за древните гърци. Следователно те могли да решават и по-общата задача: Да се построи с линийка и пергел квадрат, равнолицев с даден многоъгълник. Така се стига и до задачата за квадратурата на кръга.
Едно от най-старите сведения за нея дължим на Плутарх (I – II в). Според него известният философ Анаксагор (500 – 428 г. пр.н.е.), намирайки се в затвора, където разполагал с много време за размишления, успял да реши задачата за квадратурата на кръга. Днес знаем, че това не е вярно, но в древността това твърдение разпалвало умовете на матеманиците, а също и на много лаици. Дори „бащата на комедията“ Аристофан посвещава на тази задача един „епизод“ от комедията „Птици“. Вероятно Аристофан е познавал хора, които са давали наивни решения на задачата, и е решил да се пошегува с тях.

Случаите на погрешни решения на задачата за квадратурата на кръга са твърде много. Известният коментатор на съчиненията на Аристотел – Симплиций (VI в.), отбелязва, че „и Антифон, и Хипократ са смятали, че са решили задачата за квадратурата на кръга, но и двамата еднакво са се заблуждавали“. Антифон вписвал многоъгълници в даден кръг и увеличавал броя на страните им. Считал, че при това страните на многоъгълника ще съвпаднат със съответните им дъги. Хипократ намерил фигури (наречени по-късно лунички на Хипократ), заградени от дъги на окръжности, чиято квадратура с линийка и пергел е възможна. Това според него означава, че с линийка и пергел може да се построи квадрат, равнолицев с дадена луничка на Хипократ.
Освен тази задача в древността възникват и другите две знамените задачи за построение – задачата за удвояването на куба и задачата за трисекцията на ъгъла. Задачите стават изключително известни поради простото им формулиране и безуспешното им решаване. Почти всички видни математици посвещават много сили и време на тези задачи. Почти век преди да се докаже нерешимостта им, Френската академия на науките излиза със следното решение: „Академията постанови от днес нататък да не се разглеждат предоставяните ѝ решения на задачите за квадратурата на кръга, удвояването на куба и трисекцията на ъгъла, а също и машините, считани от техните изобретатели за осъществяващи вечно движение.“
Но не всички усилия, свързани с решаването на задачата за квадратурата на кръга, отиват напразно. Във връзка с тази задача математиците изучават числото π и създават ценни методи, които прилагат и в други области на науката.
Източници
[редактиране | редактиране на кода]- Ив. Чобанов, Г. Паскалев – Знаменити задачи на древността, изд. „Народна просвета“, С., 1982.
- Хр. Караниколов, Т. Тонков – Забележителни константи в математиката, изд. „Наука и изкуство“, С., 1989.