Singolarità ad anello
Una singolarità ad anello (in inglese ring singularity o ringularity) è la singolarità gravitazionale di un buco nero rotante, o un buco nero di Kerr, chiamata così perché ha la forma di un anello.[1]
Descrizione di una singolarità ad anello
[modifica | modifica wikitesto]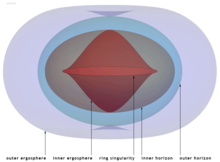
Quando un corpo sferico non rotante di raggio critico collassa sotto la propria gravità, secondo la teoria della relatività generale collasserà in un singolo punto. Questo non è il caso di un buco nero rotante (un buco nero di Kerr). La distribuzione di massa di un corpo rotante fluido non è sferica (ha un rigonfiamento equatoriale), e ha momento angolare non nullo. Poiché un punto non può supportare la rotazione o il momento angolare in fisica classica (la relatività generale è considerata classica nel senso che non rispetta la fisica quantistica), la forma minima della singolarità che può supportare queste proprietà è invece un anello con spessore nullo ma raggio diverso da zero, e questo anello viene chiamato singolarità di Kerr o ringularity.
L'effetto di trascinamento rotazionale di un buco nero rotante, descritto dalla metrica di Kerr, fa sì che lo spaziotempo nelle vicinanze dell'anello subisca una curvatura nella direzione di movimento dell'anello. In effetti questo significa che diversi osservatori posti attorno a un buco nero di Kerr a cui viene chiesto di indicare il centro di gravità apparente del buco possono puntare a diversi punti sull'anello. Gli oggetti che cadono cominceranno ad acquisire momento angolare dall'anello prima di raggiungerlo effettivamente, e il percorso seguito da un raggio di luce perpendicolare (che inizialmente viaggia verso il centro dell'anello) curverà nella direzione del movimento dell'anello prima di intersecarsi con l'anello.
Attraversabilità e nudità
[modifica | modifica wikitesto]Un osservatore che attraversa l'orizzonte degli eventi di un buco nero non rotante e non carico (di Schwarzschild) non può evitare la singolarità centrale, che si trova nel futuro di ogni linea di universo all'interno dell'orizzonte. Quindi non si può evitare la spaghettificazione da parte delle forze di marea della singolarità centrale.
Questo non è necessariamente vero con un buco nero di Kerr. Un osservatore che cade in un buco nero di Kerr può essere in grado di evitare la singolarità centrale facendo un uso intelligente dell'orizzonte degli eventi interno associato a questa classe di buchi neri. Ciò rende teoricamente (ma probabilmente non pratico)[2] possibile che il buco nero di Kerr agisca come una sorta di wormhole, forse anche un wormhole attraversabile.[3]
La singolarità di Kerr come modello di wormhole
[modifica | modifica wikitesto]La singolarità di Kerr può anche essere usata come strumento matematico per studiare il "problema delle linee di campo" del wormhole. Se una particella viene fatta passare attraverso un wormhole, le equazioni di continuità per il campo elettrico suggeriscono che le linee del campo non dovrebbero essere interrotte. Quando una carica elettrica passa attraverso un wormhole, le linee del campo di carica della particella sembrano emanare dalla bocca di ingresso e la bocca di uscita guadagna un deficit di densità di carica a causa del principio di Bernoulli. (Per la massa, la bocca di ingresso guadagna densità di massa e la bocca di uscita ottiene un deficit di densità di massa.) Poiché una singolarità di Kerr ha la stessa caratteristica, consente di studiare anche questo problema.
Esistenza di singolarità ad anello
[modifica | modifica wikitesto]Ci si aspetta generalmente che, poiché l'usuale collasso a una singolarità puntiforme sotto la relatività generale coinvolge condizioni arbitrariamente dense, gli effetti quantistici possono diventare significativi e impedire la formazione della singolarità (quantum fuzz). Senza effetti gravitazionali quantistici, ci sono buone ragioni per sospettare che la geometria interna di un buco nero rotante non sia la geometria di Kerr. L'orizzonte degli eventi interno della geometria di Kerr probabilmente non è stabile, a causa dell'infinito spostamento verso il blu della radiazione in caduta.[4] Questa osservazione è stata supportata dall'indagine sui buchi neri carichi che hanno mostrato un simile comportamento di "spostamento blu infinito".[5] Sebbene sia stato fatto molto lavoro, il collasso gravitazionale realistico degli oggetti in buchi neri rotanti e la geometria risultante continuano a essere un argomento di ricerca attivo.[6][7][8][9][10]
Note
[modifica | modifica wikitesto]- ^ Paul Sukys, Lifting the Scientific Veil, Rowman & Littlefield, 1999, p. 533, ISBN 978-0-8476-9600-0.
- ^ Roy Kerr: Spinning Black Holes (Lecture at the University of Canterbury, timecode 49m8s
- ^ William J. III Kaufmann, The Cosmic Frontiers of General Relativity, Boston, Toronto, Little, Brown and Company (Inc.), 1977, p. 178,9.
- ^ Roger Penrose, Battelle Rencontres, a cura di de Witt, New York, W. A. Benjamin, 1968, p. 222.
- ^ E. Poisson e W. Israel, Internal structure of black holes, in Phys. Rev. D, vol. 41, n. 6, 1990, pp. 1796-1809, Bibcode:1990PhRvD..41.1796P, DOI:10.1103/PhysRevD.41.1796, PMID 10012548.
- ^ Shahar Hod e Tsvi Piran, The Inner Structure of Black Holes, in Gen. Rel. Grav., vol. 30, n. 11, 1998, p. 1555, Bibcode:1998GReGr..30.1555H, DOI:10.1023/A:1026654519980, arXiv:gr-qc/9902008.
- ^ Amos Ori, Oscillatory Null Singularity inside Realistic Spinning Black Holes, in Physical Review Letters, vol. 83, n. 26, 1999, pp. 5423-5426, Bibcode:1999PhRvL..83.5423O, DOI:10.1103/PhysRevLett.83.5423, arXiv:gr-qc/0103012.
- ^ Patrick R Brady, Serge Droz e Sharon M Morsink, The late-time singularity inside non-spherical black holes, in Physical Review D, vol. 58, n. 8, 1998, p. 084034, Bibcode:1998PhRvD..58h4034B, DOI:10.1103/PhysRevD.58.084034, arXiv:gr-qc/9805008.
- ^ Igor D. Novikov, Developments in General Relativity: Black Hole Singularity and Beyond, in Texas in Tuscany, 2003, pp. 77-90, Bibcode:2003tsra.symp...77N, DOI:10.1142/9789812704009_0008, ISBN 978-981-238-580-2, arXiv:gr-qc/0304052.
- ^ Lior M. Burko e Amos Ori, Are physical objects necessarily burnt up by the blue sheet inside a black hole?, in Physical Review Letters, vol. 74, n. 7, 13 febbraio 1995, pp. 1064-1066, Bibcode:1995PhRvL..74.1064B, DOI:10.1103/PhysRevLett.74.1064, PMID 10058925, arXiv:gr-qc/9501003.
Bibliografia
[modifica | modifica wikitesto]- Kip Thorne, Buchi neri e salti temporali. L'eredità di Einstein, Castelvecchi, 2017, ISBN 978-8832821949.
- Matt Visser, Lorentzian Wormholes: from Einstein to Hawking, AIP Press, 1995.