Teorema del coseno

In geometria, il teorema del coseno esprime la relazione tra la lunghezza dei lati di un triangolo e il coseno di uno dei suoi angoli. Può essere considerato una generalizzazione del teorema di Pitagora al caso di triangoli non rettangoli. Questo teorema, dimostrato già dal persiano Al-Kashi, è noto anche, specialmente in Francia, come teorema di Al-Kashi o anche, specialmente in Italia, come teorema di Carnot, dal nome del matematico francese Lazare Carnot, anche se in realtà il teorema è stato reso popolare dal francese François Viète.

Il teorema

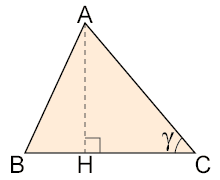
Con riferimento alla figura a lato, si desidera trovare la lunghezza di un lato di un qualsiasi triangolo, essendo note le lunghezze degli altri due lati e l'ampiezza dell'angolo tra essi compreso. Si ha:

${\overline {AB}}^{2}={\overline {AC}}^{2}+{\overline {BC}}^{2}-2\cdot {\overline {AC}}\cdot {\overline {BC}}\cos \gamma .$

Dimostrazione con il teorema di Pitagora

Applicando il teorema di Pitagora al triangolo rettangolo $AHB,$ si ha:

${\overline {AB}}^{2}={\overline {AH}}^{2}+{\overline {BH}}^{2},$

Risolvendo il triangolo rettangolo $AHC$ si ha anche:

${\overline {AH}}={\overline {AC}}\sin \gamma .$

Vale inoltre

${\overline {BH}}={\overline {BC}}-{\overline {HC}}={\overline {BC}}-{\overline {AC}}\cos \gamma .$

Sostituendo nella prima uguaglianza si ottiene:

${\overline {AB}}^{2}={\overline {AC}}^{2}\sin ^{2}\gamma +{\overline {BC}}^{2}+{\overline {AC}}^{2}\cos ^{2}\gamma -2{\overline {BC}}\cdot {\overline {AC}}\cos \gamma .$

Per la relazione fondamentale $\sin ^{2}\gamma +\cos ^{2}\gamma =1,$ questa equazione può essere semplificata in:

${\overline {AB}}^{2}={\overline {AC}}^{2}+{\overline {BC}}^{2}-2{\overline {BC}}\cdot {\overline {AC}}\cos \gamma .$

Nel caso di un triangolo rettangolo, ossia con $\gamma =\pi /2,$ il terzo addendo del secondo membro è nullo e si ricade nel teorema di Pitagora, mentre se il triangolo è ottusangolo ($\gamma >\pi /2$) la dimostrazione procede allo stesso modo, con la differenza che in questo caso:

${\overline {HC}}={\overline {AC}}\cos(\pi -\gamma )=-{\overline {AC}}\cos \gamma$

e quindi si trova nuovamente

${\overline {BH}}={\overline {BC}}+{\overline {HC}}={\overline {BC}}-{\overline {AC}}\cos \gamma .$

Dimostrazione con vettori

Si considerino, con riferimento alla figura precedente, i vettori:

${\vec {a}}={\vec {BC}};$

${\vec {b}}={\vec {AC}};$

${\vec {c}}={\vec {AB}}.$

Si può quindi scrivere che:

${\vec {c}}={\vec {b}}-{\vec {a}}.$

Calcolando il modulo al quadrato di ambo i membri si ottiene:

$|{\vec {c}}|^{2}=|{\vec {b}}-{\vec {a}}|^{2}=({\vec {b}}-{\vec {a}})\cdot ({\vec {b}}-{\vec {a}}),$

$|{\vec {c}}|^{2}=|{\vec {b}}|^{2}+|{\vec {a}}|^{2}-2{\vec {b}}\cdot {\vec {a}},$

dove ${\vec {b}}\cdot {\vec {a}}$ è il prodotto scalare tra ${\vec {b}}$ e ${\vec {a}}$. Usando infine il fatto che ${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}||{\vec {b}}|\cos \gamma$ si ricava

$c^{2}=a^{2}+b^{2}-2ab\cos \gamma .$

Voci correlate

• Coseno
• Trigonometria
• Triangolo
• Teorema di Pitagora
• Teorema dei seni
• Teorema della corda

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sul teorema del coseno

Collegamenti esterni

• Teorema del coseno, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) law of cosines, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Teorema del coseno, su MathWorld, Wolfram Research.

Controllo di autorità	Thesaurus BNCF 21832