四分音
四分音![]() playとは、半音階の通常の音符間の中間の音高であり、(聴覚的にまたは対数的に)全音(長2度)の半分である半音の半分の音程。
playとは、半音階の通常の音符間の中間の音高であり、(聴覚的にまたは対数的に)全音(長2度)の半分である半音の半分の音程。

四分音の種類
[編集]
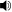 Play or
Play or 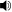 play
play「四分音」という用語は、様々な異なる、しかし大きさが非常に似た音程を指しうる。例えば、17世紀や18世紀の理論家の何人かはシャープと異名同音的に区別されたフラット(例: D♯–E♭)の距離を述べるためにこの用語を使用した[2]。四分音音階つまり24平均律 (24-TET)では、四分音は50セント、振動数比21/24、約1.0293であり、オクターブを24の等しい段(平均律)に分割する。この音律では、四分音は最小の段である。よって半音は2つの音程からなり、3つの音程は「3つの四分音」(three-quarter tone) ![]() play 、中立2度、短三度の半分をなす。
play 、中立2度、短三度の半分をなす。
純正律では、四分音は第七倍音準拠四分音、36:35 (48.77セント)または33:32 (53.27セント)、16:15か25:24の半音の約半分で表すことができる。35:36の比は1.23セントだけ24平均律よりも狭い。この比はまた短三度 (6:5)と第七倍音準拠短三度 (7:6)の違いでもある。
四分音とそれに近い音程は、他の多くの平均律体系でも起こる。22平均律は、四分音よりもわずかに広い54.55セントの音程を持ち、53平均律は45.28セントの音程を持つがこれはわずかに狭い。72平均律も平均律の四分音を持ち、72は24で割れるので3つの四分音音階を持つ。
アメリカ合衆国出身の現代音楽の作曲家のベン・ジョンストンは、純正律の第七倍音準拠四分音に対応するため、小さな"7"の記号を音高が49セント下げられたことを示す臨時記号として使い、また逆さまの"∠"の記号を音高が49セントつまり36/35の比[3]上げた事を示すために使う。[4]ジョンストンは 上向きと下向きの矢印を33/32の比つまり53セント上げる、または下げることを表すために用いる。[3]
楽器での四分音の演奏
[編集]
現在作製される楽器の多くは12音音階のために設計されているため、四分音の演奏に全て使えるわけではない。時には特別な演奏技法が必要である。
マルクノイキルヒェンen:MarkneukirchenのFritz Schüller (1883–1977)による四分音クラリネットen:quarter tone clarinet といった四分音を演奏するための実験楽器が開発されてきた。
ピッチ・シフト(en:Pitch shifter (audio processor))のような音響信号処理効果を用いれば、その他の楽器でも四分音の演奏に使える。
一組のそれぞれ四分音ずつずらして調律した通常の楽器は、いくつかの四分音音楽の演奏のために使う。四分音ピアノは開発されているが、これは実質的には2つのピアノを1つのケースに積み重ね、片方を四分音分高く調律したものである。複数段のキーボードに別々のステップが設計された微分音調律を伴う音階をあてがうことも、普通に行われる。
一段の鍵盤を複雑に割った四分音ピアノの開発も第二次世界大戦前は行われていたが、今は行われていない。
四分音が演奏できないケース
[編集]- 通常のフレットを持つ弦楽器(ギターのチョーキングやトレモロアーム奏法などを除く)
- ピアノ、標準の調律
- オルガン、通常に調律された時
- シンセサイザー (設計上可能でない時)
- 旋律打楽器、調律されておらず標準的な技法が使われた時
- アコーディオン、通常に調律された時
四分音が演奏できるケース
[編集]- アコーディオン (フリーリードの調律をあらかじめ四分音下げる、または上げた場合)
- シンセサイザー (設計上可能なとき)
- 無フレット弦楽器 (フレットのある弦楽器でもチョーキングや特別な調律を用いたときは可能)
- 四分音のフレットを持つ弦楽器
- スライド金管楽器 (トロンボーン・ゼフュロス)
- バルブ金管楽器(トランペット、 ホルン、 チューバ)
- 木管楽器、特別な指使いやフィンガー・ビブラート(en:Finger_vibrato#Wind_instruments)を使用した時
- ハーモニカ、フィンガー・ビブラートを使用するとき
- アコーディオン、通常に調律されていて、低い音域でフィンガー・ビブラートを使用する時、または備え付けボタンで音程を下げたとき
- ハープ、特別な調律の時
- ピアノ、特別な調律の時
- オルガン、そのために調律される時
- 旋律打楽器、調律した時や、特殊な技法を用いる時
- テルミン
四分音を用いた音楽
[編集]多くの作曲家が四分音や、または19世紀の音楽理論家ミーハーイール・ミシャーカen:Mikha'il Mishaqah[5] が最初に提案した「四分音階」(「24平均律」)を含む音楽を作曲したことで知られる。例えばピエール・ブーレーズ、en:Julián Carrillo、 en:Mildred Couper、アルベルト・ヒナステラ、ジェラール・グリゼー、 アロイス・ハーバ、リュビツァ・マリッチ、チャールズ・アイヴズ、トリスタン・ミュライユ、クシシュトフ・ペンデレツキ、ジャチント・シェルシ、カールハインツ・シュトックハウゼン、en:Tui St. George Tucker、イワン・ヴィシネグラツキー、ヤニス・クセナキスなどが挙げられる。 (四分音の作品の一覧en:List of quarter tone piecesも参照)
しかし、四分音を認めながら、その後離れる作曲家も珍しくない。前述のピエール・ブーレーズは四分音の使用を後年放棄している。橋本國彦は「幼年の歌」一作だけである。芥川也寸志は「ヒロシマのオルフェ」で四分音を全面的に展開したが、その後は使用していない。また「四分音より、三分音のほうがしっくりくる」作曲家もいて、戸田邦雄とモーリス・オアナがその類に入る。また四分音をさらに割った八分音を駆使する作曲家もおり、クリス・デンクやブライアン・ファーニホウが用いている。
中東の音楽
[編集]現在の西欧音楽での四分音の使用が最近のことで実験的な現象である一方、四分音やその他の微分音の音程はイラン(ペルシア)やアラブ世界やアルメニアやトルコやアッシリアやクルディスタンやその近隣で、何世紀にも渡り旋法の中で重宝されてきた。それは現代の中近東ポピュラー音楽でさえ、調律に微分音を用いて続いている。

多くのアラブのマカーム(旋法)は以下の4分の3の大きさの音程を含む。なお便宜上、四分音下がるフラットはqと表記するが、この表記は一般的なものではない。 [6]
- ショール (バヤーティー)
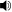 play
play
- شور (بیاتی)
- D Eq F G A Bq C D
- شور (بیاتی)
- フサイニー
- シーガー
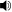 play
play
- سيكاه
- Eq F G A Bq C D Eq
- سيكاه
- ラースト
 play
play
- راست
- C D Eq F G A Bq C
- 下降形ではB♭がBqに置き換わる
- C D Eq F G A Bq C
- راست
- アジャム
- サバー
 play
play
- صبا
- D Eq F G♭ A B♭ C D
- صبا
イスラーム哲学者で科学者でもあるファーラービーは、多くの四分音を挙げて、多くの音程について音楽についての著作で解説した。
アッシリア/シリア教会音楽音階:[7]
- 1 - Qadmoyo (バヤーティー)
- 2 - Trayono (Hussayni)
- 3 - Tlithoyo (シーガー)
- 4 - Rbi‘oyo (ラースト)
- 5 - Hmishoyo
- 6 - Shtithoyo (アジャム)
- 7 - Shbi‘oyo
- 8 - Tminoyo
四分音音階
[編集]
 Play
Play
 Play
Playアラビア語で「ジャドワル」gadwalとして知られる[8] 四分音音階は中東で18世紀発展し、19世紀シリアの最初の詳細な記載の多くは音階が24平均律であると述べている。[9] この音階の発明はミーハーイール・ミシャーキーen:Mikhail Mishaqaに帰せられ、彼の著作「音楽の技巧についてのアミール・シハーブへの論文」(al-Risāla al-shihābiyya fi 'l-ṣinā‘a al-mūsīqiyya) はこの話題に捧げられるとともに、彼の師ムハンマド・アル=アッタールen:Muhammad al-‘Attār 師(1764-1828)が この考えにすでに親しんでいた者の大勢のうちの一人であったことを明らかにした。 [10]
四分音音階は、当初はアラビア音楽の理論的な構成物と見做されたかもしれない。四分音は音楽家に四分音の数による音程を議論し比較するための「概念的な見取り図」(conceptual map)を与えるが、当時から音楽理論における指示が主流の要件であったのでもしかしたらこれが理論への新たな興味を伴う理由の1つかもしれない。[9]
以前はある旋法のなかの音高は13世紀のサフィーッディーン・アル=ウルマウィーen:Safi 'I-Din al-Urmawiが開発した17の音からなる音階から選ばれた。 [10]
ポピュラー音楽
[編集]日本の多楽器演奏家で実験楽器発明家の尾上祐一は、24平均律四分音調律の自身のギターで開発した。[11] 四分音ギターは、アロイス・ハーバの発明である。それにならって、ノルウェーのバンドTNTのギターリストのロニー・ル・テクロen:Ronni Le Tekroは三番目のスタジオ・アルバムIntuitionで四分音間隔のギターを使用した。
古代ギリシアのテトラコルド
[編集]
 Play
Play古代ギリシアのエンハルモニオンのゲノス (en:enharmonic genus) のテトラコルドは、一つの二全音en:ditoneつまりおおよその長三度と二つの微分音に分けられる半音を構成する。アリストクセネスen:Aristoxenosやディデュモスen:Didymosなどは、半音を二つのだいたいの同サイズの四分音の音程に分割されるものとして示し、また別の古代ギリシアの理論家は微分音をエンハルモニオンのゲノスの半音の不等分割の結果(つまり一つは4分の1より小さくもう一つは大きい)もとのして示した。.[12]
平均律での音程のサイズ
[編集]これは、24音平均律音階の一般的な音程のサイズと、アロイス・ハーバ (中立三度など)とイワン・ヴィシネグラツキー (長四度など)によって提案された音程名である。
| 音程名 | サイズ(段) | サイズ (セント) | midi | 純正比 | 純正 (セント) | midi | 誤差 |
|---|---|---|---|---|---|---|---|
| オクターブ | 24 | 1200 | 2:1 | 1200.00 | 0.00 | ||
| 半減オクターブen:semidiminished octave | 23 | 1150 | 2:1 | 1200.00 | −50.00 | ||
| 超長七度en:supermajor seventh | 23 | 1150 | 35:18 | 1151.23 | −1.23 | ||
| 長七度en:major seventh | 22 | 1100 | 15:8 | 1088.27 | +11.73 | ||
| 中立七度en:neutral seventh | 21 | 1050 | 11:6 | 1049.36 | +0.64 | ||
| 短七度en:minor seventh | 20 | 1000 | 16:9 | 996.09 | +3.91 | ||
| 超長六度en:supermajor sixth/下短七度en:subminor seventh | 19 | 950 | 7:4 | 968.83 | −18.83 | ||
| 長六度en:major sixth | 18 | 900 | 5:3 | 884.36 | +15.64 | ||
| 中立六度en:neutral sixth | 17 | 850 | 18:11 | 852.59 | −2.59 | ||
| 短六度 | 16 | 800 | 8:5 | 813.69 | −13.69 | ||
| 下短六度en:subminor sixth | 15 | 750 | 14:9 | 764.92 | −14.92 | ||
| 完全五度 | 14 | 700 | 3:2 | 701.95 | −1.95 | ||
| 短五度en:minor fifth | 13 | 650 | 16:11 | 648.68 | +1.32 | ||
| 小さな七の三全音en:septimal tritone | 12 | 600 | 7:5 | 582.51 | +17.49 | ||
| 長四度en:major fourth | 11 | 550 | 11:8 | 551.32 | −1.32 | ||
| 完全四度 | 10 | 500 | 4:3 | 498.05 | +1.95 | ||
| 十三の長三度 | 9 | 450 | 13:10 | 454.21 | −4.21 | ||
| 七の長三度en:septimal major third | 9 | 450 | 9:7 | 435.08 | +14.92 | ||
| 長三度 | 8 | 400 | 5:4 | 386.31 | +13.69 | ||
| 11の中立三度en:neutral third | 7 | 350 | 11:9 | 347.41 | +2.59 | ||
| 短三度 | 6 | 300 | 6:5 | 315.64 | −15.64 | ||
| 七の短三度en:septimal minor third | 5 | 250 | 7:6 | 266.88 | −16.88 | ||
| 十一の短三度 | 5 | 250 | 15:13 | 247.74 | +2.26 | ||
| 七の全音en:septimal whole tone | 5 | 250 | 8:7 | 231.17 | +18.83 | ||
| 大全音en:major tone | 4 | 200 | 9:8 | 203.91 | −3.91 | ||
| 小全音en:minor tone | 4 | 200 | 10:9 | 182.40 | +17.60 | ||
| 大きい十一の中立二度en:neutral second、 | 3 | 150 | 11:10 | 165.00 | −15.00 | ||
| 小さい十一の中立二度、 | 3 | 150 | 12:11 | 150.64 | −0.64 | ||
| 15:14半音 | 2 | 100 | 15:14 | 119.44 | −19.44 | ||
| 全音階的半音en:diatonic semitone、純正律 | 2 | 100 | 16:15 | 111.73 | −11.73 | ||
| 21:20半音 | 2 | 100 | 21:20 | 84.47 | +15.53 | ||
| 28:27半音 | 1 | 50 | 28:27 | 62.96 | −12.96 | ||
| 七の四分音en:septimal quarter tone | 1 | 50 | 36:35 | 48.77 | +1.23 |
12平均律から24平均律への移調は、多くの音程の近似を許容する。音程は特に中立二度 en:neutral secondや中立三度en:neutral thirdや(11:8)比つまり11番目のハーモニックにとても近く合致する。七の短三度en:septimal minor thirdと七の長三度en:septimal major thirdにはむしろ不完全に近似する。(13:10)と(15:13)の比は、13番目のハーモニックに関係して、とても近く合致する。総体的に、24平均律はよりも7番目のハーモニックよりも11番目のハーモニックにより近く合致するとみなせる。
関連項目
[編集]- 音律
- 微分音
- en:List of quarter tone pieces(四分音の作品の一覧)
- en:List of meantone intervals(微分音の音程の一覧)
- en:Tonsilabos
脚注
[編集]- ^ a b Boatwright, Howard (1965). "Ives' Quarter-Tone Impressions", Perspectives of New Music 3, no. 2 (Spring-Summer): pp. 22–31; citations on pp. 27–28; reprinted in Perspectives on American Composers, edited by Benjamin Boretz and Edward T. Cone, pp. 3-12, New York: W. W. Norton, 1971, citation on pp. 8–9. "These two chords outlined above might be termed major and minor."
- ^ Julian Rushton, "Quarter-tone", The New Grove Dictionary of Music and Musicians, second edition, edited by en:Stanley Sadie and John Tyrrell (London: Macmillan Publishers, 2001).
- ^ a b Fonville, John (Summer, 1991). "Ben Johnston's Extended Just Intonation: A Guide for Interpreters", p.114, Perspectives of New Music, Vol. 29, No. 2, pp. 106-137.
- ^ Douglas Keislar; Easley Blackwood; John Eaton; Lou Harrison; Ben Johnston; Joel Mandelbaum; William Schottstaedt. p.193. "Six American Composers on Nonstandard Tunnings", Perspectives of New Music, Vol. 29, No. 1. (Winter, 1991), pp. 176-211.
- ^ Touma, Habib Hassan (1996). The Music of the Arabs, p.16. Trans. Laurie Schwartz. Portland, Oregon: Amadeus Press. ISBN 0-931340-88-8.
- ^ Spector, Johanna (May 1970). “Classical 'Ud Music in Egypt with Special Reference to Maqamat” (GIF). Ethnomusicology 14 (2): 243–257. doi:10.2307/849799. JSTOR 00141836. [リンク切れ]
- ^ Asaad, Gabriel (1990). Syria's Music Throughout History
- ^ "Classical 'Ud Music in Egypt with Special Reference to Maqamat", p.246. Johanna Spector. Ethnomusicology, Vol. 14, No. 2. (May, 1970), pp. 243-257.
- ^ a b Marcus, Scott (1993)."The Interface between Theory and Practice: Intonation in Arab Music", Asian Music, Vol. 24, No. 2. (Spring - Summer, 1993), pp. 39-58.
- ^ a b Maalouf, Shireen (2003). "Mikhii'il Mishiiqa: Virtual Founder of the Twenty-Four Equal Quartertone Scale", Journal of the American Oriental Society, Vol. 123, No. 4. (Oct. - Dec., 2003), pp. 835-840.
- ^ Yuichi Onoue on hypercustom.com Archived 2015年11月8日, at the Wayback Machine.
- ^ Chalmers, John H. Jr. (1993). Divisions of the Tetrachord. Hanover, NH: Frog Peak Music. ISBN 0-945996-04-7 Chapter 5, Page 49
関連書籍
[編集]- Bartolozzi, Bruno (1967). New Sounds for Woodwind. London, New York: Oxford University Press.
- Bousted, Donald (2002). "Microtonality, the Recorder and the Quarter-Tone Recorder Manual". The Recorder Magazine 22, no. 3 (Fall): 99–102.
- Bousted, Donald (2005). "Next Step Quarter-Tone Resources: Melody". The Recorder Magazine 25, no. 3 (Fall): 88–91.
- Caravan, Ronald R. (1979). Preliminary Exercises and Etudes in Contemporary Techniques for Clarinet: Introductory Material for the Study of Multiphonics, Quarter Tones, and Timbre Variation. [Oswego, N.Y.]: Ethos Publications.
- Ellis, Don (1975). Quarter Tones: A Text with Musical Examples, Exercises and Etudes. Plainview, N.Y.: Harold Branch Pub. Co.
- MacDonald, John (1822). A Treatise on the Harmonic System Arising from the Vibrations of the Aliquot Divisions of Strings According to the Gradual Progress of the Notes from the Middle, to the Remote Extremes: Explaining Simply, by Curved Delineations, the Manner in Which the Harmonic Tones, Half and Quarter Notes, Are Generated and Produced on Every Corresponding Part of the String; and under a Copious Explanatory Description Illustrated by Musical and Appropriate Plates, Giving an Easy and Familiar Adaptation of the Whole to the Purposes of Composition and Instrumental Music, and More Particularly, to the Practice of the Violin, Tenor, Violoncello and Double Bass, on All the Strings, and in Every Compass of These Instruments, by Every Practical Mode of Execution; with Some Musical Animadversions Introductory of the General Subject, Briefly Alluding to the Rise and Progress of Music, and to the Corrections of Temperament: and Stating Various Improvements of Instruments, Experimentally Ascertained: Concluding with an Application or Two of the Principle of Musical Notes, to Purposes of Utility, and a Reference to Terms Less Generally Noticed. London: Printed for the Author, and Sold by T. Preston.
- Möllendorff, Willi, and Joe Monzo (2001). Music with Quarter-Tones: Experiences at the Bichromatic Harmonium. [United States]: J. Monzo.
- Rees, Carla (2007). "Eva Kingma and the Quarter-Tone Flute". Pan: The Flute Magazine 26, no. 4:23-29.
- Rewoldt, Todd (2000). "Altissimo Quarter-Tones for the Alto Saxophone". Saxophone Symposium 25:56–69.
外部リンク
[編集]- "quarter-tone / 24-edo", TonalSoft.com.
- IVAN WYSCHNEGRADSKY'S MANUAL OF QUARTER-TONE HARMONY