Stelsel van lineaire vergelijkingen

In de wiskunde is een stelsel van lineaire vergelijkingen, ook lineair systeem, een aantal lineaire vergelijkingen in dezelfde onbekenden.
Een voorbeeld van een stelsel van drie lineaire vergelijkingen is
met de drie onbekenden . Een oplossing van een lineair systeem is de toewijzing van getallen aan de variabelen, zodanig dat tegelijkertijd aan alle vergelijkingen wordt voldaan. Een oplossing voor het bovenstaande lineaire systeem is:
Deze oplossing is voor alle drie vergelijkingen geldig.[1]
De theorie van lineaire systemen is in de wiskunde een tak van de lineaire algebra. Numerieke algoritmen voor het vinden van oplossingen vormen een belangrijk onderdeel van de numerieke lineaire algebra. Dergelijke methoden spelen een belangrijke rol in verschillende vakgebieden, waaronder bouwkunde, economie, elektrotechniek, informatica, natuurkunde en scheikunde. Een systeem van niet-lineaire vergelijkingen kan vaak door een lineair systeem worden benaderd. Dat wordt lineariseren genoemd en is een handige techniek bij het maken van wiskundige modellen of computersimulaties van een relatief complex systeem.
Algemene vorm
[bewerken | brontekst bewerken]Een algemeen stelsel van lineaire vergelijkingen met onbekenden kan worden geschreven als
Hierin zijn de onbekenden en de coëfficiënten van het stelsel; zijn de constante termen.
Vaak zijn de coëfficiënten en onbekenden reële of complexe getallen, maar gehele getallen, rationale getallen en elementen van andere algebraïsche structuren komen ook voor.
Vectorvergelijking
[bewerken | brontekst bewerken]Een nuttige zienswijze is om elke onbekende als een gewicht voor een kolomvector in een lineaire combinatie te zien.
Men kan hierdoor gebruikmaken van de theorie van de vectorruimten of meer algemeen van modulen. De verzameling van alle mogelijke lineaire combinaties van de vectoren aan de linkerzijde van de vergelijking heet bijvoorbeeld het lineaire opspansel en de vergelijkingen hebben een oplossing precies wanneer de vector aan de rechterzijde van de vergelijking binnen dit lineaire opspansel valt. Als elke vector binnen dit opspansel precies één uitdrukking als een lineaire combinatie van de gegeven vectoren aan de linkerzijde heeft, dan is de oplossing uniek. In ieder geval heeft het opspansel een basis van lineair onafhankelijke vectoren die precies één expressie garanderen; het aantal vectoren in deze basis, de dimensie, kan niet groter zijn dan of maar dit aantal kan ook kleiner zijn. Dit is belangrijk, want als wij onafhankelijke vectoren hebben, is een oplossing gegarandeerd, ongeacht de rechterkant van de vergelijking, anders is dit niet het geval.
Matrixvergelijking
[bewerken | brontekst bewerken]De vectorvergelijking komt met de matrixvergelijking
overeen, waarin een -matrix is, een kolomvector met elementen en een kolomvector met elementen.
Een methode voor het oplossen van het stelsel is met Gauss-eliminatie, dus met vegen van de uitgebreide matrix Deze ontstaat door aan de matrix de kolomvector als extra kolom toe te voegen:
Als de matrix vierkant is, dus als en de rang ervan gelijk is aan , kan de oplossing van de vergelijkingen met de inverse matrix worden gevonden:
Oplossingsverzameling
[bewerken | brontekst bewerken]
Een oplossing van een stelsel van lineaire vergelijkingen is een toekenning van waarden aan de variabelen zodanig dat aan alle vergelijkingen wordt voldaan. De verzameling van alle mogelijke oplossingen wordt de oplossingsverzameling genoemd.
Een lineair systeem kan zich op een van drie mogelijke manieren gedragen:
- Het systeem heeft oneindig veel oplossingen, het stelsel is onbepaald.
- Het systeem heeft een enkele unieke oplossing.
- Het systeem heeft geen oplossingen, dus is inconsistent.
Deze drie mogelijke gevallen kunnen gekoppeld worden aan twee stellingen. De eerste geeft informatie over het bestaan van oplossingen, de tweede over het aantal:
- Stelling 1: Er is voor een stelsel een oplossing, dan en slechts dan als de rang van gelijk is aan de rang van de met de kolomvector uitgebreide matrix .
- Stelling 2: Indien het stelsel oplosbaar is, is het aantal vrije oplossingen gelijk aan het aantal variabelen verminderd met de rang van .
Indien de uitgebreide matrix in echelonvorm staat, zijn eventuele vrije oplossingen op eenvoudige wijze te herkennen: het zijn die variabelen die in de echelonvorm geen leidende 1 in hun kolom hebben. Bij een strijdig stelsel zal . Dit betekent dat, door de vergelijkingen te herschrijven, een vergelijking kan worden bekomen waarin alle coëfficiënten van de onbekenden nul zijn, maar met een rechterlid verschillend van nul.
Om de rang van een matrix te kunnen bepalen, kan de uitgebreide matrix het best in echelonvorm worden gezet.
Meetkundige interpretatie
[bewerken | brontekst bewerken]Voor een systeem met twee variabelen en bepaalt elke lineaire vergelijking een lijn in het -vlak. Omdat een oplossing van een stelsel van lineaire vergelijkingen moet voldoen aan alle vergelijkingen die deel uitmaken van dit stelsel, is de oplossingsverzameling de doorsnede van deze lijnen. Deze doorsnede kan in dit geval bestaan uit een lijn, een enkel punt of uit de lege verzameling.
Voor drie variabelen bepaalt elke lineaire vergelijking een vlak in de driedimensionale ruimte. De oplossingsverzameling is de doorsnede van deze vlakken en kan bestaan uit een vlak, een lijn, een enkel punt of uit de lege verzameling.
Voor variabelen bepaalt elke lineaire vergelijking een hypervlak in de -dimensionale ruimte. De oplossingsverzameling is de doorsnede van deze hypervlakken en kan bestaan uit een vlak van elke dimensie.
Algemeen gedrag
[bewerken | brontekst bewerken]De oplossingsverzameling van een stelsel lineaire vergelijkingen wordt bepaald door de verhouding tussen het aantal vergelijkingen en het aantal onbekenden:
- Meestal heeft een lineair stelsel met minder vergelijkingen dan onbekenden oneindig veel oplossingen, maar het kan ook geen oplossing hebben. Het stelsel heet onbepaald.
- Meestal heeft een lineair stelsel met evenveel vergelijkingen als onbekenden een unieke oplossing. Het stelsel kan echter ook strijdig zijn, zodat er geen oplossing is, of er kan afhankelijkheid in het stelsel zijn, waardoor er in feite minder vergelijkingen zijn dan onbekenden.
- Meestal heeft een lineair stelsel met meer vergelijkingen dan onbekenden geen enkele oplossing. Zo'n stelsel heet overbepaald.
In het eerste geval is de dimensie van de oplossingsverzameling meestal gelijk aan waarin staat voor het aantal variabelen en voor het aantal vergelijkingen.
De onderstaande afbeeldingen illustreren dit voor het geval dat er twee variabelen zijn:

|
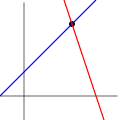
|

|
| Een vergelijking | Twee vergelijkingen | Drie vergelijkingen |
Het eerste systeem heeft oneindig veel oplossingen, namelijk alle punten op de blauwe lijn. Het tweede systeem heeft een enkele unieke oplossing, namelijk het snijpunt van de twee lijnen. Het derde systeem heeft geen oplossing, want de drie lijnen delen geen gemeenschappelijk punt.
Houd er rekening mee dat de afbeeldingen hierboven alleen het meest voorkomende geval tonen. Het is mogelijk dat een lineair stelsel van twee vergelijkingen en twee onbekenden geen enkele oplossing heeft (bijvoorbeeld als de twee lijnen parallel aan elkaar lopen). Ook kan een stelsel van drie vergelijkingen en twee onbekenden wel degelijk oplosbaar zijn (bijvoorbeeld als de drie lijnen elkaar in een punt snijden). In het algemeen zal een stelsel van lineaire vergelijkingen zich anders dan verwacht gedragen als de vergelijkingen lineair afhankelijk zijn, of indien twee of meer van de vergelijkingen inconsistent zijn.
Oplossing voor een inconsistent stelsel
[bewerken | brontekst bewerken]Bij praktische toepassing zoals in de landmeetkunde worden overtallige metingen gedaan om blunders in de metingen op te kunnen sporen. Door meetruis levert dit echter ook zonder blunders een inconsistent stelsel van vergelijkingen op. Om toch een eenduidige oplossing te krijgen worden de metingen vereffend met de kleinstekwadratenmethode. Bij normaal verdeelde meetruis geeft dit de beste schatting voor de onbekenden.
Voorbeeld
[bewerken | brontekst bewerken]Als tussen drie punten de hoogteverschillen gemeten zijn en van het eerste punt de hoogte bekend is, dan kan het volgende stelsel van waarnemingsvergelijkingen opgesteld worden:
met de vector met metingen, de vector met onbekenden en een vector met de meetfouten waarvan de verwachtingswaarde nul is:
De oplossing kan dan worden gevonden door:
Wanneer niet alle metingen ongecorreleerd zijn en dezelfde precisie hebben moet er gewogen worden met de inverse covariantiematrix . De oplossing wordt dan:
Voetnoten
[bewerken | brontekst bewerken]- ↑ De lineaire algebra, zoals in dit artikel wordt besproken, is een reeds lang gevestigde wiskundige discipline, waarvoor zeer veel bronnen zijn. Bijna al het materiaal in dit artikel kan worden gevonden in een willekeurig leerboek lineaire algebra op universitair niveau.
Literatuur
[bewerken | brontekst bewerken]- (en) Anton Howard, Elementary Linear Algebra (Applications Version), ISBN 978-0471669593, Wiley International, 9e editie, 2005
- (en) Steven J. Leon, Linear Algebra With Applications, Pearson Prentice Hall, ISBN 978-0131857858, 7e editie, 2006
- (en) Gilbert Strang, Linear Algebra and Its Applications, Brooks Cole, ISBN 978-0030105678, 4e editie, 2005