தொடர்வரிசையின் எல்லை

ஓரலகு வட்டத்தைச் சுற்றி வரையப்பட்ட ஒழுங்கு n-பக்க பல்கோணிகளின் சுற்றளவுகளின் தொடர்வரிசையின் எல்லை அவ்வலகு வட்டத்தின் சுற்றளவாக ( $2\pi$) இருக்கும். இது அலகு வட்டத்துக்குள் வரையப்பட்ட ஒழுங்கு n-பக்க பல்கோணிகளுக்கும் பொருந்தும்

$n$	$n\times \sin \left({\tfrac {1}{n}}\right)$
1	0.841471
2	0.958851
...
10	0.998334
...
100	0.999983

நேர்ம முழு எண் ${\textstyle n}$ பெரிதாகப் பெரிதாக, ${\textstyle n\times \sin \left({\tfrac {1}{n}}\right)}$ இன் மதிப்பு ${\textstyle 1}$ க்கு மிகவருகில் நெருங்கும். எனவே ${\textstyle n\times \sin \left({\tfrac {1}{n}}\right),}$ உறுப்புகளாலான தொடர்தொடர்வரிசையின் எல்லை, ${\textstyle 1}$ ஆகும் ($\lim _{n\to \infty }n\times \sin \left({\tfrac {1}{n}}\right)=1.$)

கணிதத்தில் ஒரு தொடர்வரிசையின் எல்லை (limit of a sequence) என்பது அத்தொடர்வரிசையின் உறுப்புகள் அணுகும் மதிப்பைக் குறிக்கும். எல்லைக்கு, $\lim$ என்ற குறியீடு ($\lim _{n\to \infty }a_{n}$) பயன்படுத்தப்படுகிறது. ஒரு தொடர்வரிசைக்கு எல்லைமதிப்பு இருக்குமானால், அது ஒருங்கும் தொடர்வரிசை எனப்படும்; ஒருங்காத தொடர்வரிசைகள், விரிதொடர்வரிசைகள் எனப்படும். பகுவியலின் அடிப்படைக் கருத்தாக அமைந்துள்ள இதன் அடிப்படையிலேதான் பகுவியல் முழுமையும் அமைந்துள்ளது.

எந்தவொரு மெட்ரிக் வெளி அல்லது இடத்தியல் வெளியிலும் தொடர்வரிசையின் எல்லையை வரையறுக்கமுடியுமென்றாலும், இக்கருத்துரு மெய்யெண்களில்தான் முதலில் எதிர்கொள்ளப்பட்டது.

வரலாறு

முதன்முதலில் கிரேக்க மெய்யியலாளர் எலியாவின் சீனோ, அவரது தோற்ற முரண்களில் எல்லை காணும்முறையை முறைப்படுத்தினார்.

லியூசிப்பஸ், டெமோக்கிரட்டிசு, ஆன்ட்டிபோன்,, நீடியோசின் யூடாக்சசு, அர்க்கிமெடெசு ஆகிய அறிஞர்கள் நீக்கல் முறையை மேம்படுத்தி, ஒரு முடிவுறாத் தொடர்வரிசையைத் தோராயப்படுத்தி பரப்பளவையும், கனவளவையும் கண்டுபிடித்தனர். இன்று பெருக்குத் தொடர் என அழைக்கப்படும் தொடரின் கூட்டுத்தொகை காணும் வழியை அர்க்கிமெடெசு கண்டறிந்தார்

கணிதவியலாளர் கிரகோரி டி செயின்ட்-வின்சென்ட், முதன்முதலாகப் பெருக்குத் தொடரின் எல்லையின் வரையறையை வெளியிட்டார் (Opus Geometricum (1647))

பியாட்ரோ மென்கோலி என்ற இத்தாலியக் கணிதவியலாளர் தொடர்வரிசையின் எல்லையின் நவீன கருத்தை தனது ஆய்வுகளில் முன்னதாகவே கணித்திருந்தார்.

ஐசாக் நியூட்டன் தொடர்கள் குறித்து ஆய்வு செய்திருந்தார் (Analysis with infinite series -1669 இல் எழுதப்பட்டு, கையெழுத்துப் படியாக இருந்து, 1711 இல் வெளியிடப்பட்டது; Method of fluxions and infinite series -1671 எழுதப்பட்டு, 1736 இல் ஆங்கில மொழிபெயர்ப்பாக வெளியாகி பின்னாளில் இலத்தீன் மூலப்படி பின்னாளில் வெளியானது; Tractatus de Quadratura Curvarum -1693இல் எழுதப்பட்டு, 1704இல் அவரது Optiksஇல் பின்சேர்க்கையாக வெளியானது). அவரது பிந்தைய ஆய்வுகளில், ${\textstyle o\to 0}$ எனும்போது எல்லை காண்பதன்மூலம் ஈருறுப்பு விரிவு ${\textstyle (x+o)^{n}}$ ஐ நேரியல் படுத்தினார்.

18 ஆம் நூற்றாண்டில், கணிதவியலாளர் ஆய்லர் போன்ற கணிதவியலாளர்கள் சில விரிதொடர்களின் கூட்டுத்தொகை காண்பதில் வெற்றிபெற்றனர். 18 ஆம் நூற்றாண்டின் இறுதியில் கணிதவியலாளர் லாக்ராஞ்சி, சரியான முயற்சியின்மையே நுண்கணிதத்தில் மேலதிக மேம்படையாதன் காரணம் என்ற கருத்தைத் தெரிவித்தார் (Théorie des fonctions analytiques -1797) முதன்முதலாக கணிதவியலாளர் காஸ், ஒரு தொடரானது ஒரு குறிப்பிட்ட எல்லைக்கு ஒருங்குவதற்குத் தேவையான நிபந்தனைகளைக் கண்டறிந்தார்.

எல்லையின் தற்கால வரையறை, கணிதவியலாளர்கள் பெர்னார்டு பொல்சானோ (Der binomische Lehrsatz, Prague 1816), கார்ல் வியர்ஸ்ட்ராஸ் (1870களில்) கண்டறியப்பட்டது.

மெய்யெண்கள்

நீல நிறத்தில் ஒருங்குதொடர், {a_n}. n இன் மதிப்பு அதிகரிக்க, அதிகரிக்க தொடர்வரிசையானது, '0' எல்லையை நெருங்குவதைக் காணலாம்.

மெய்யெண்களில், $(x_{n})$ எனும் தொடர்வரிசையின் உறுப்புகள் $L$ என்ற எண்ணுக்கு மிகமிக அருகில் நெருங்கினால், $L$ ஆனது $(x_{n})$ இன் எல்லை எனப்படும்.

எடுத்துக்காட்டுகள்

• $x_{n}=c;$ ${\textstyle c}$ ஒரு மாறிலியெனில்,

$x_{n}\to c$.

• $x_{n}={\frac {1}{n}}$ எனில்,

$x_{n}\to 0$.

• $x_{n}={\frac {1}{n}},$ $n$ ஓர் [[நிகரி (கணிதம்)|இரட்டைப்படை எண்; மேலும் $n$ ஓர் ஒற்றைப்படை எண்ணாக இருக்கும்போது $x_{n}={\frac {1}{n^{2}}}$ எனில்,

$x_{n}\to 0$. ($n$ ஒற்றையெண் எனில், $x_{n+1}>x_{n}$ என்பது இங்கு பொருத்தமற்றது.)

• எந்தவொரு மெய்யெண்ணுக்கும், தசமத் தோராயங்களை எடுப்பதன்மூலம், அதே எண்ணுக்கு ஒருங்கும் ஒரு தொடர்வரிசையை அமைக்க முடியும்:

எடுத்துக்காட்டாக, ${\textstyle 0.3,0.33,0.333,0.3333,\dots }$ என்ற தொடர்வரிசையின் எல்லை, ${\textstyle {\frac {1}{3}}}$ அல்லது பதின்ம உருவகிப்பில் ${\textstyle 0.3333\dots }$ ஆகும்.

$$0.3333...:=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {3}{10^{k}}}$$

• எல்லாத் தொடர்வரிசைகளுக்கும் எல்லை காண்பது எளிதானதாக இருக்காது. எடுத்துக்காட்டாக, எண் e ஐ எல்லையாகக்கொண்ட $\lim _{n\to \infty }\left(1+{\tfrac {1}{n}}\right)^{n}$தொடர்வரிசையும் கூட்டு-பெருக்குச் சராசரி தொடர்வரிசையும் இதற்கு எடுத்துக்காட்டுகளாகும். இத்தகைய தொடர்வரிசைகளின் எல்லைகளைக் காண்பதற்கு பிழிவுத் தேற்றம் பயன்படுகிறது.

வரையறை

ஒவ்வொரு மெய்யெண் $\varepsilon >0$ க்கும், $n\geq N$ என்ற ஒவ்வொரு இயல் எண்ணுக்கும்

$|x_{n}-x|<\varepsilon$

என்பதை நிறைவு செய்யும்விதத்தில் $N$ என்ற ஒரு இயல் எண் இருக்குமானால்,

$(x_{n})$ தொடர்வரிசையின் எல்லை $x$ எனப்படுகிறது.

மேலும் இக்கூற்று குறியீட்டில் கீழுள்ளவாறு எழுதப்படுகிறது:

$x_{n}\to x$ அல்லது

$\lim _{n\to \infty }x_{n}=x$

அதாவது, $\varepsilon$ அளவு நெருக்கத்தில், தொடர்வரிசையின் உறுப்புகள், அதேயளவு நெருக்கத்தில் எல்லை மதிப்பிற்கு அருகிலிருக்கும்; $(x_{n})$ தொடர்வரிசையானது $x$ என்ற எல்லைமதிப்பிற்கு "ஒருங்கும்" எனப்படுகிறது.

குறியீட்டில்:

$\forall \varepsilon >0\left(\exists N\in \mathbb {N} \left(\forall n\in \mathbb {N} \left(n\geq N\implies |x_{n}-x|<\varepsilon \right)\right)\right)$.

$(x_{n})$ தொடர்வரிசையின் எல்லை $x$ எனில், அது ஒரு ஒருங்கும் தொடரென்பதோடு, $x$ மட்டுமே அதன் ஒரேயொரு எல்லையாக இருக்கும். அவ்வாறு ஒரேயொரு முடிவுறு எல்லையைக் கொண்டிருக்காவிட்டால், $(x_{n})$ ஒரு விரிதொடராகும். சிலசமயங்களில், பூச்சியத்தை எல்லையாகக் கொண்ட தொடர்வரிசை, "சுழித் தொடர்" எனப்படும்.

விளக்கப்படங்கள்

• 
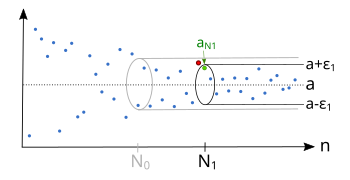
  $a$ என்ற எல்லைக்கு ஒருங்கும் தொடர்வரிசை.
• 
  எந்தவொரு $\varepsilon >0$ மதிப்புக்கும், $N_{0}$ க்குப் பிறகு, தொடர்வரிசை முழுவதுமாக எப்சலான் குழலுக்குள் - $(a-\varepsilon ,a+\varepsilon )$ அமையுமாறு ஒரு குறிப்பிட்ட $N_{0}$ இருக்கும்.
• 
  அதைவிடச் சிறிய $\varepsilon _{1}>0$ மதிப்பிற்கும் $N_{1}$, க்குப் பிறகு, தொடர்வரிசை முழுவதும் எப்சலான்_1 குழலுக்குள் - $(a-\varepsilon _{1},a+\varepsilon _{1})$இருக்குமாறு ஒரு $N_{1}$ இருக்கும்.
• 
  ஒவ்வொரு $\varepsilon >0$ க்கும் எப்சலான் குழலைவிட்டு வெளியே இருக்கக்கூடிய தொடர்வரிசை உறுப்புகள் மிகச் சிலவே.

பண்புகள்

மெய்யெண் தொடர்வரிசைகளின் எல்லை பற்றிய முக்கிய பண்புகள்:

• எல்லையுள்ள தொடர்வரிசைகள் தனித்துவமானவை.

• வழக்கமான அடிப்படைக் கணிதச் செயல்கள் தொடர்வரிசை எல்லைகளுக்கும் பொருந்தும்.

$\lim _{n\to \infty }a_{n},$ $\lim _{n\to \infty }b_{n}$ இரண்டும் உண்டென்றால்:

$\lim _{n\to \infty }(a_{n}\pm b_{n})=\lim _{n\to \infty }a_{n}\pm \lim _{n\to \infty }b_{n}$

$\lim _{n\to \infty }ca_{n}=c\cdot \lim _{n\to \infty }a_{n}$

$\lim _{n\to \infty }(a_{n}\cdot b_{n})=\left(\lim _{n\to \infty }a_{n}\right)\cdot \left(\lim _{n\to \infty }b_{n}\right)$

$\lim _{n\to \infty }\left({\frac {a_{n}}{b_{n}}}\right)={\frac {\lim \limits _{n\to \infty }a_{n}}{\lim \limits _{n\to \infty }b_{n}}}$ ($\lim _{n\to \infty }b_{n}\neq 0$ ஆக இருந்தால்)

$\lim _{n\to \infty }a_{n}^{p}=\left(\lim _{n\to \infty }a_{n}\right)^{p}$

• ${\textstyle f}$ என்பது ஒரு [[தொடர்ச்சியான சார்பாக இருந்து அதன் எல்லை $\lim _{n\to \infty }x_{n}$ உம் இருக்குமானால், $\lim _{n\to \infty }f\left(x_{n}\right)$ உம் இருக்கும்.

எந்தவொரு மெய்யெண் சார்பு ${\textstyle f}$ உம், தொடர்வரிசைகளின் எல்லைகளை மாறாமல் காப்பதாக "இருந்தால், இருந்தால் மட்டுமே" அது ஒரு தொடர்ச்சியான சார்பாக இருக்க முடியும்.

• $N$ ஐ விடப் பெரிய அனைத்து $n$ இன் மதிப்புகளுக்கும் $a_{n}\leq b_{n}$ எனில்,

$\lim _{n\to \infty }a_{n}\leq \lim _{n\to \infty }b_{n}$.

• $N$ ஐ விடப் பெரிய அனைத்து $n$ இன் மதிப்புகளுக்கும் $a_{n}\leq c_{n}\leq b_{n}$; மேலும் $\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }b_{n}=L$ எனில்,

$\lim _{n\to \infty }c_{n}=L$. (பிழிவுத் தேற்றம்)

• $N$ ஐ விடப் பெரிய அனைத்து $n$ இன் மதிப்புகளுக்கும், $a_{n}$ ஒரு வரம்புடைய, ஒருபோக்குத் தொடர்வரிசை எனில், அது ஒரு ஒருங்கு தொடராகும். (ஒருபோக்கு ஒருங்கல் தேற்றம்)

• ஒரு தொடர்வரிசையின் துணைத்தொடர்வரிசைகள் அனைத்தும் ஒருங்கல் தொடர்வரிசைகளாக "இருந்தால், இருந்தால் மட்டுமே," தாய்த்தொடர்வரிசையும் ஒருங்கல் தொடராக இருக்கும்.

• ஒவ்வொரு துணைத் தொடர்வரிசைக்கும் அதே மதிப்பிற்கு ஒருங்கும் அதனுடைய துணைத் தொடர்வரிசை இருக்குமானால், தாய்த் தொடர்வரிசையும் அதே எல்லைமதிப்புக்கு ஒருங்கும்.

முடிவுலி எல்லைகள்

குறியீட்டில் முடிவிலி எல்லை:

$x_{n}\to \infty$, அல்லது

$\lim _{n\to \infty }x_{n}=\infty$,

கீழ்வரும் கூற்று உண்மையாக இருந்தால், $(x_{n})$ தொடர்வரிசையானது "முடிவிலியை நெருங்குகிறது அல்லது அணுகுகிறது" எனப்படும்:

ஒவ்வொரு மெய்யெண் $K$ க்கும், $n\geq N$ ($N$ ஒரு இயல் எண்) என்றவாறுள்ள ஒவ்வொரு இயல் எண்ணுக்கும்

$x_{n}>K$

அதாவது தொடர்வரிசையின் ஒவ்வொரு உறுப்பும் நிலையான $K$ என்ற மதிப்பைவிடப் பெரியதாக இருக்கும்.

இதனைக் குறியீட்டில் பின்வருமாறு எழுதலாம்:

$\forall K\in \mathbb {R} \left(\exists N\in \mathbb {N} \left(\forall n\in \mathbb {N} \left(n\geq N\implies x_{n}>K\right)\right)\right)$.

எதிர்ம முடிவிலி எல்லை:

குறியீடு:

$x_{n}\to -\infty$, அல்லது

$\lim _{n\to \infty }x_{n}=-\infty$

நிறைவு செய்யவேண்டிய கூற்று:

ஒவ்வொரு மெய்யெண் $K$ க்கும், $n\geq N$ ($N$ ஒரு இயல் எண்) என்றவாறுள்ள ஒவ்வொரு இயல் எண்ணுக்கும்

$x_{n}<K$;

அதாவது தொடர்வரிசையின் ஒவ்வொரு உறுப்பும் நிலையான $K$ என்ற மதிப்பைவிடச் சிறியதாக இருக்கும்.

இதனைக் குறியீட்டில் பின்வருமாறு எழுதலாம்:

$\forall K\in \mathbb {R} \left(\exists N\in \mathbb {N} \left(\forall n\in \mathbb {N} \left(n\geq N\implies x_{n}<K\right)\right)\right)$.

$-\infty$ அல்லது $+\infty$ ஆக எல்லையைக் கொண்ட தொடர்வரிசைகள் விரிதொடர்வரிசைகளாகும். ஆனால் விரிதொடர்வரிசைகள் அனைத்தும், $-\infty$ அல்லது $+\infty$ ஐ எல்லையாகக் கொண்டிருக்கத் தேவையில்லை.

இதற்கு ஒரு எடுத்துக்காட்டு:

$x_{n}=(-1)^{n}$

மெட்ரிக் வெளிகள்

வரையறை

மெட்ரிக் வெளி $(X,d)$ இலுள்ள ஒரு புள்ளி $x$, தொடர்வரிசை $(x_{n})$ இன் எல்லையாக இருக்க வேண்டுமானால் பின்வரும் கூற்று உண்மையாக இருக்கவேண்டும்:

ஒவ்வொரு மெய்யெண் $\varepsilon >0$ மற்றும் ஒவ்வொரு இயல் எண் $n$ க்கும்,

$d(x_{n},x)<\varepsilon ,\forall n\geq N$ என்ற கட்டுப்பாட்டை நிறைவுசெய்யும் ஒரு இயல் எண் $N$ இருக்கவேண்டும்.

இது குறியீட்டில் பின்வருமாறு தரப்படுகிறது.:

$\forall \varepsilon >0\left(\exists N\in \mathbb {N} \left(\forall n\in \mathbb {N} \left(n\geq N\implies d(x_{n},x)<\varepsilon \right)\right)\right)$.

$X=\mathbb {R} ,$ $d(x,y)=|x-y|$ எனவும் இருந்தால் மெட்ரிக் வெளியின் தொடர்வரிசைகளின் எல்லையின் வரையறையானது, மெய்யெண்களில் தொடர்வரிசையின் எல்லையுடன் ஒத்தமைகிறது

பண்புகள்

• ஒரு தொடர்வரிசைக்கு எல்லை இருக்குமானால், அவ்வெல்லை தனித்ததாக இருக்கும். அதாவது ஒரு தொடர்வரிசைக்கு ஒரேயொரு எல்லை மட்டுமே இருக்கும். ஏனெனில், வெவ்வேறான இரு புள்ளிகள் நேர்ம தூரத்தால் பிரிக்கப்பட்டுள்ளதோடு, இத்தூரத்தின் அளவில் பாதியைவிடச் சிறியதாகவுள்ள $\varepsilon$ மதிப்புகளுக்கு, தொடர்வரிசையின் உறுப்புகள் இவ்விரு புள்ளிகளிலிருந்தும் $\varepsilon$ தூரத்தில் இருக்கமுடியாது.

• தொடர்ச்சியான சார்பு f என்ற தொடர்ச்சியான சார்புக்கு, $\lim _{n\to \infty }x_{n}$ இருக்குமானால்,

$\lim _{n\to \infty }f(x_{n})=f\left(\lim _{n\to \infty }x_{n}\right)$ ஆக இருக்கும்.

சார்பு f ஆனது, தொடர்வரிசைகளின் எல்லைகளை மாறாமல் காப்பதாக "இருந்தால், இருந்தால் மட்டுமே" அது ஒரு தொடர்ச்சியான சார்பாக இருக்க முடியும்.

கோசி தொடர்வரிசை

நீல நிறத்தில் காட்டப்பட்டுள்ள கோசியின் தொடர்வரிசை: (x_n). படத்தில், n இன் மதிப்பு அதிகரிக்க, அதிகரிக்க, தொடர்வரிசை $x_{n}$, ஒரு எல்லைப் புள்ளியை நோக்கி நெருங்குவதைக் காணலாம். மெய்யெண்களிலமைந்த ஒவ்வொரு கோசி தொடர்வரிசையும், ஒரு எல்லைமதிப்பிற்கு ஒருங்கும்.

கோசி தொடர்வரிசை என்பது, போதுமானவளவு சில துவக்க உறுப்புகளை நீக்கிய பின்னர் இதர உறுப்புகள் அறுதியாக ஒன்றுக்கொன்று நெருக்கமாக அமைகின்றவாறுள்ள உறுப்புகளைக்கொண்ட தொடர்வரிசையாகும். மெட்ரிக் வெளியிலும், குறிப்பாக மெய்ப் பகுவியலிலும், தொடர்வரிசைகள் குறித்த ஆய்வுகளுக்கு கோசி தொடர்வரிசை முக்கியானமானதாகும். ஒரு தொடர்வரிசையின் ஒருங்கல்தன்மையைக் கண்டறியப் பயன்படுகிறது. ஒரு தொடர்வரிசையானது கோசி தொடர்வரிசையாக, "இருந்தால், இருந்தால் மட்டுமே," அத்தொடர்வரிசை, ஒருங்கல் தொடர்வரிசையாக இருக்க முடியும்.

இடவியல் வெளிகள்

வரையறை

இடவியல் வெளி $(X,\tau )$ இலுள்ள ஒரு புள்ளி $x\in X$, தொடர்வரிசை $\left(x_{n}\right)_{n\in \mathbb {N} }$ இன் எல்லை அல்லது எல்லைப் புள்ளியாக இருக்க வேண்டுமானால் பின்வரும் கூற்று உண்மையாக இருக்கவேண்டும்:

$x$ ஒவ்வொரு இடவெளி அண்மையகத்திற்கும் ($U$), ஒவ்வொரு இயல் எண் $n\geq N$க்கும்,

$x_{n}\in U$ என்ற கட்டுப்பாட்டை நிறைவுசெய்யும் ஒரு இயல் எண் $N$ இருக்கவேண்டும்.

$(X,d)$ என்ற மெட்ரிக் வெளியில் $d$ஆல் பிறப்பிக்கப்பட்ட இடவியல் வெளி $\tau$ எனில், இடவியல் வெளிகளில் வரையறுக்கப்படும் தொடர்வரிசையின் எல்லை வரையறையானது மெட்ரிக் வெளியில் வரையறுக்கப்பட்டதுடன் பொருந்துகிறது.

பண்புகள்

ஒரு ஹவுசுடார்ப் வெளியில், தொடர்வரிசைகளின் எல்லைகள் தனித்தவையாக இருக்கும். அதாவது ஒரு தொடர்வரிசைக்கு ஒரேயொரு எல்லை மட்டுமே இருக்கும். ஆனால் ஹவுசுடார்ப் வெளியல்லாதவற்றில் அவ்வாறிருப்பதில்லை. குறிப்பாக $x,$ $y$ ஆகியவை இடவெளியில் வேறுபடுத்த முடியாத இரு புள்ளிகள் எனில், $x$ க்கு ஒருங்கும் ஒரு தொடர்வரிசை $y$ ஆகவும் ஒருங்கும். இதேபோல, $y$ க்கு ஒருங்கும் ஒரு தொடர்வரிசை $x$ ஆகவும் ஒருங்கும்.

ஒன்றுக்கு மேற்பட்டசுட்டெண்கொண்ட தொடர்வரிசை

ஒன்றுக்கு மேற்பட்ட சுட்டெண்ணுள்ள தொடர்வரிசைகளுக்கும் எல்லைகளைக் காணலாம். எடுத்துக்காட்டாக, இரு சுட்டெண்களுள்ள இரட்டைத் தொடர்வரிசை $(x_{n,m})$. இத்தொடர்வரிசையில், n , m இரண்டும் மிகப் பெரியதாக அதிகரிக்க, அதிகரிக்க தொடர்வரிசையானது, $L$ க்கு மிகமிக அருகில் நெருங்குமானால், இதற்கு எல்லை உண்டு.

எடுத்துக்காட்டுகள்

• $x_{n,m}=c$ (${\textstyle c}$ ஒரு மாறிலி) எனில், $x_{n,m}\to c$.
• $x_{n,m}={\frac {1}{n+m}}$ எனில் $x_{n,m}\to 0$.
• $x_{n,m}={\frac {n}{n+m}}$ எனில், எல்லை இருக்காது. ${\textstyle n,}$ and ${\textstyle m}$ இரண்டும் அதிகரிக்கும் சார் வேகத்தைப் பொறுத்து, தொடர்வரிசையானது, ${\textstyle 0,}$ ${\textstyle 1}$ ஆகிய இரண்டுக்கும் இடைப்பட்ட எந்தவொரு மதிப்புக்கும் அருகாக நெருங்கும்.

வரையறை

$(x_{n,m})$ என்ற தொடர்வரிசையின் "இரட்டை எல்லை" $x$ ,கீழ்வருமாறு குறியீட்டில் எழுதப்படுகிறது:

$x_{n,m}\to x$, அல்லது

$\lim _{\begin{smallmatrix}n\to \infty \\m\to \infty \end{smallmatrix}}x_{n,m}=x$,

கீழுள்ள நிபந்தனை நிறைவு செய்யப்படுமானால், $(x_{n,m})$ என்ற தொடர்வரிசையின் "இரட்டை எல்லை"யாக $x$ இருக்கும்:

$\varepsilon >0$ என்ற மெய்யெண் ஒவ்வொன்றுக்கும், மேலும் $n,m\geq N$ என்றமையும் ஒவ்வொரு சோடி இயல் எண்களுக்கும்,

$|x_{n,m}-x|<\varepsilon$

என்பதை நிறைவுசெய்யும்வகையில் $N$ என்ற ஒரு இயல் எண் இருக்கவேண்டும்.

அதாவது, ஒவ்வொரு $\varepsilon$ அளவு நெருக்கத்திற்கும், தொடர்வரிசையின் உறுப்புகள், அதேயளவு நெருக்கத்தில் எல்லை மதிப்பிற்கு அருகிலிருக்கும். $(x_{n,m})$ தொடர்வரிசையானது $x$ என்ற எல்லைமதிப்பிற்கு "ஒருங்கும்" அல்லது "நெருங்கும்" எனப்படுகிறது.

இதுவே குறியீட்டில் பின்வருமாறு எழுதப்படுகிறது:

$\forall \varepsilon >0\left(\exists N\in \mathbb {N} \left(\forall n,m\in \mathbb {N} \left(n,m\geq N\implies |x_{n,m}-x|<\varepsilon \right)\right)\right)$.

இரட்டை எல்லையானது, முதலில் n இல் எல்லை கண்டு, அதன் பின்னர் m இல் எல்லை காணும் "தொடர்முறை எல்லை"யிலிருந்து வேறுபட்டதாகும். ஒரு தொடர்வரிசைக்கு இரட்டை எல்லை, தொடர்முறை எல்லை என இரண்டுமே இருக்குமானால், அவற்றின் மதிப்புகள் சமமாகவே இருக்கும். இவ்விரு எல்லைகளில் ஒன்று காணத்தக்கதாக இருந்து, மற்றது இல்லாமலும் இருக்கலாம்.

முடிவிலி எல்லைகள்

இரட்டைத் தொடர்வரிசை $(x_{n,m})$ இன் முடிவிலி எல்லைக்கான குறியீடு:

$x_{n,m}\to \infty$, அல்லது

$\lim _{\begin{smallmatrix}n\to \infty \\m\to \infty \end{smallmatrix}}x_{n,m}=\infty$,

கீழுள்ள நிபந்தனை நிறைவு செய்யப்படுமானால் $(x_{n,m})$ என்ற தொடர்வரிசைக்கு எல்லை முடிவிலியாக இருக்கும்:

$K$ என்ற ஒவ்வொரு மெய்யெண்ணுக்கும், மேலும் $n,m\geq N$ என்றமையும் ஒவ்வொரு சோடி இயல் எண்களுக்கும்,

$x_{n,m}>K$ என்றவாறு $N$ என்ற ஒரு இயல் எண் இருக்கவேண்டும்.

அதாவது தொடர்வரிசையின் ஒவ்வொரு உறுப்பும் நிலையான $K$ ஐ விடப் பெரியது.

இதுவே குறியீட்டில் பின்வருமாறு தரப்படுகிறது:

$\forall K\in \mathbb {R} \left(\exists N\in \mathbb {N} \left(\forall n,m\in \mathbb {N} \left(n,m\geq N\implies x_{n,m}>K\right)\right)\right)$.

$-\infty$ எல்லை:

குறியீடு:

$x_{n,m}\to -\infty$, அல்லது

$\lim _{\begin{smallmatrix}n\to \infty \\m\to \infty \end{smallmatrix}}x_{n,m}=-\infty$,

நிறைவு செய்யப்படவேண்டிய நிபந்தனை:

$K$ என்ற ஒவ்வொரு மெய்யெண்ணுக்கும், மேலும் $n,m\geq N$ என்றமையும் ஒவ்வொரு சோடி இயல் எண்களுக்கும்,

$x_{n,m}<K$ என்றவாறு $N$ என்ற ஒரு இயல் எண் இருக்கவேண்டும்.

அதாவது தொடர்வரிசையின் ஒவ்வொரு உறுப்பும் நிலையான $K$ ஐ விடச் சிறியது.

இதுவே குறியீட்டில் பின்வருமாறு தரப்படுகிறது:

$\forall K\in \mathbb {R} \left(\exists N\in \mathbb {N} \left(\forall n,m\in \mathbb {N} \left(n,m\geq N\implies x_{n,m}<K\right)\right)\right)$.

$-\infty$ அல்லது $+\infty$ ஐ நெருங்கும் தொடர்வரிசைகள் விரிதொடர்வரிசைகள் எனப்படுகின்றன. ஆனால் எல்லா விரிதொடர்வரிசைகளும் $-\infty$ அல்லது $+\infty$ ஐ நெருங்காது. இதற்கொரு எடுத்துக்காட்டு:

$x_{n,m}=(-1)^{n+m}$

புள்ளிவாரியான எல்லைகளும் சீரான எல்லைகளும்

$(x_{n,m})$ என்ற இரட்டைத் தொடர்வரிசைக்கு ஏதாவது ஒரு சுட்டெண்ணுக்கான எல்லையைக் காணலாம். எடுத்துக்காட்டாக, $n\to \infty$ என எடுத்துக்கொண்டு, $(y_{m})$ என்ற ஒற்றைத் தொடர்வரிசையைப் பெறலாம். இவ்வாறு எல்லை காண்பதில், இரு எல்லைகள் உள்ளன. ஒன்று "புள்ளிவாரியான எல்லை" ( pointwise limit); மற்றது "சீரான எல்லை" (uniform limit).

புள்ளிவாரியான எல்லை

குறியீடு:

$x_{n,m}\to y_{m}\quad {\text{pointwise}}$, அல்லது

$\lim _{n\to \infty }x_{n,m}=y_{m}\quad {\text{pointwise}}$,

நிறைவு செய்யவேண்டிய நிபந்தனை:

$\varepsilon >0$ என்ற ஒவ்வொரு மெய்யெண்ணுக்கும், $m$ என்ற ஒவ்வொரு நிலையான இயல் எண்ணுக்கும், மேலும் $n\geq N$ என்றமையும் ஒவ்வொரு இயல் எண் $n$க்கும்:

$|x_{n,m}-y_{m}|<\varepsilon$ என்றிருக்குமாறு ஒரு இயல் எண் $N(\varepsilon ,m)>0$ இருக்கும்.

குறியீட்டில் இந்நிபந்தனை:

$\forall \varepsilon >0\left(\forall m\in \mathbb {N} \left(\exists N\in \mathbb {N} \left(\forall n\in \mathbb {N} \left(n\geq N\implies |x_{n,m}-y_{m}|<\varepsilon \right)\right)\right)\right)$.

இந்த எல்லையை காணமுடிந்தால், $(x_{n,m})$ தொடர்வரிசையானது "புள்ளிவாரியாக ஒருங்கல் தொடர்வரிசை" எனப்படும்; அதன் எல்லை அல்லது ஒருங்கு மதிப்பு $(y_{m})$ ஆகும்.

சீரான எல்லை

குறியீடு:

$x_{n,m}\to y_{m}\quad {\text{uniformly}}$,

$\lim _{n\to \infty }x_{n,m}=y_{m}\quad {\text{uniformly}}$,

$x_{n,m}\rightrightarrows y_{m}$, or

${\underset {n\to \infty }{\mathrm {unif} \lim }}\;x_{n,m}=y_{m}$,

நிறைவுசெய்ய வேண்டிய நிபந்தனை:

$\varepsilon >0$ என்ற ஒவ்வொரு மெய்யெண்ணுக்கும், $m$ என்ற ஒவ்வொரு இயல் எண்ணுக்கும், மேலும் $n\geq N$ என்றமையும் ஒவ்வொரு இயல் எண் $n$க்கும்:

$|x_{n,m}-y_{m}|<\varepsilon$ என்றிருக்குமாறு ஒரு இயல் எண் $N(\varepsilon )>0$ இருக்கும்.

குறியீட்டில் இந்நிபந்தனை:

$\forall \varepsilon >0\left(\exists N\in \mathbb {N} \left(\forall m\in \mathbb {N} \left(\forall n\in \mathbb {N} \left(n\geq N\implies |x_{n,m}-y_{m}|<\varepsilon \right)\right)\right)\right)$.

இவ்வாறான எல்லை இருந்தால், $(x_{n,m})$ தொடர்வரிசையானது ஒரு சீரான ஒருங்கல் தொடர்வரிசையாகும்; அதன் சீரான ஒருங்கல் மதிப்பு $(y_{m})$ ஆகும்.

சீரான எல்லையின் வரையறையில் $N$ இன் தேர்வு, $m$ ஐச் சார்ந்திருக்காது. அதாவது $N$ இன் தேர்வு, $m$ இன் அனைத்து இயலெண் மதிப்புகளுக்கும் பொதுவானது. எனவே தொடர்வரிசையின் புள்ளிவாரியான ஒருங்கலை விடச் சீரான ஒருங்கல் வலுவான பண்பாகும். ஒரு தொடர்வரிசைக்குச் சீரான எல்லை இருந்தால், அத்தொடர்வரிசைக்குப் புள்ளிவாரியான ஒருங்கலும் இருக்கும்; மேலும் புள்ளிவாரியான ஒருங்கல் மதிப்பானது, சீரான ஒருங்கல் மதிப்புக்குச் சமமாகவும் இருக்கும்.

தொடர்முறை எல்லை

$(x_{n,m})$ என்ற இரட்டைத் தொடர்வரிசைக்கு ஏதாவது ஒரு சுட்டெண்ணுக்கான எல்லையைக் காணலாம். எடுத்துக்காட்டாக, $n\to \infty$ என எடுத்துக்கொண்டு, $(y_{m})$ என்ற ஒற்றைத் தொடர்வரிசையைப் பெறலாம். அதன் பிறகு இரண்டாவது சுட்டெண் $m\to \infty$ என எடுத்துக்கொண்டு, $y$ என்ற எண்ணைப் பெறலாம்.

குறியீட்டில்:

$\lim _{m\to \infty }\lim _{n\to \infty }x_{n,m}=\lim _{m\to \infty }y_{m}=y$.

இவ்வெல்லை, இரட்டைத் தொடர்வரிசையின் "தொடர்முறை எல்லை" (iterated limit) எனப்படுகிறது. சுட்டெண்களைத் தேர்வு செய்யும் வரிசை, இறுதி எல்லையின் மதிப்பை மாற்றும்:

$\lim _{m\to \infty }\lim _{n\to \infty }x_{n,m}\neq \lim _{n\to \infty }\lim _{m\to \infty }x_{n,m}$

இவ்வெல்லைகள் சமமாக இருப்பதற்குப் போதுமான நிபந்தனை:

$\lim _{n\to \infty }x_{n,m}=y_{m}$ ஆனது ${\textstyle m}$இல் சீரான எல்லையாக இருக்கவேண்டும்.

வெளி இணைப்புகள்

• Hazewinkel, Michiel, ed. (2001), "Limit", Encyclopedia of Mathematics, Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-1556080104
• A history of the calculus, including limits