空間填充多面體
在幾何學中,空間填充多面體是指可以獨立堆砌並無空隙且不重疊地填滿三維空間的立體。 也就是說能將該立體、及該立體的多個全等副本透過平移、旋轉和/或鏡射來填充整個三維空間。 這「填充」意味著該多面體的所有實體組合在一起時構成了三維空間的劃分。 事實上,任何三維空間的週期性密鋪或堆砌體都可以透過平移一個基本單元多面體來生成。
| 部分的空間填充多面體 | |
|---|---|
 空間填充十三面體 |
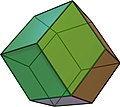 菱形十二面體 |
 三角化截角四面體 |
 星形四角化菱形十二面體 |
例子
编辑任何平行多面體都是空間填充多面體,更具體地說是五種平行多面體的任何一種平行多面體,例如菱形十二面體都是空間填充多面體。[2]:29
立方體可以獨立堆滿空間,因此是一種空間填充多面體,且立方體是唯一具有這種性質的柏拉圖立體。[3]:183—184雖然正四面體和正八面體也可以以交錯組合的方式填滿空間,但兩者都無法獨立填滿空間,因此不能算是空間填充多面體。[4]:210[5]:232
對於唯一一種能填滿空間的某種類型多面提還有一個例子,也就是異相雙三角柱。異相雙三角柱可以獨立堆滿空間,因此是一種空間填充多面體[6],且是唯一具有這種性質的约翰逊多面体[7][8]
只有五種凸正多邊形面多面體是空間填充多面體,分別為正三角柱、正六角柱、立方體、截角八面體[9][10]和異相雙三角柱[11]。
菱形十二面體[9][10]、菱形六角化十二面體以及最密堆積中出現的梯形菱形十二面體[4]:203—207都是空間填充多面體。
以正鑲嵌圖的單位為底面的柱體,如正三角形鑲嵌對應正三角形底面的三角柱、正方形鑲嵌對應正方形底面的正四角柱和正六邊形鑲嵌對應正六邊形底面的六角柱所構成的柱體也是空間填充多面體。因為若將這些柱體以對應正鑲嵌圖的方式排列成的單層晶格可以層層疊起來,以填滿三維空間。
歷史
编辑最早討論空間填充多面體的學者是亚里士多德。亚里士多德在其著作《論天》中宣稱四面體可以填滿空間,但事實上並非如此。[1]
在1974年至1980年間,邁克爾·戈德堡(Michael Goldberg)試圖對空間填充多面體進行詳盡的編目。根據戈德堡的說法,有27個不同的充填空間六面體,當中包括了除了五角錐外的所有7種六面體。在34種拓樸結構有明顯差異的凸七面體中[12],有16種是空間填充多面體,其可以56種不同的方式填充空間。而八面體至少可以49種不同的方式填充空間。在1980年之前的論文中,空間填充多面體有40個是十一面體、16個是十二面體、4個是十三面體、8個是十四面體、沒有十五面體、一個十六面體(最初由福普爾(Föppl)發現[13][5]:234)、2個十七面體、1個十八面體、6個二十面體、2個二十一面體、5個二十二面體、2個二十三面體、1個二十四面體以及一個被認為是最多面的空間填充多面體二十六面體。[1]隨後在1980年,P·恩格爾(P. Engel)又發現了17到38個面的另外172個空間填充多面體,之後也持續發現更多空間填充多面體。[5]:234—235大約在1990年,P·施密特(P. Schmitt)發現了一種非凸的非週期空間填充多面體。[1]1993年,約翰·何頓·康威發現了一種僅以非週期的方式填充空間的空間填充凸多面體,稱為施密特—康威—丹澤爾雙柱體(Schmitt–Conway–Danzer biprism)。[14]
參見
编辑參考文獻
编辑- ^ 1.0 1.1 1.2 1.3 Weisstein, Eric W. Space-Filling Polyhedron. mathworld.wolfram.com. [2023-12-01]. (原始内容存档于2024-01-07) (英语).
- ^ Coxeter, H.S.M. Regular Polytopes 3rd. New York: Dover. 1973 [1948].
- ^ Gardner, M. Martin Gardner's Sixth Book of Mathematical Diversions from Scientific American. Scientific American. University of Chicago Press. 1983. ISBN 9780226282503. LCCN lc83012332.
- ^ 4.0 4.1 4.2 Steinhaus, H. Mathematical Snapshots. Dover Recreational Math Series. Dover Publications. 1999. ISBN 9780486409146. LCCN 99033052.
- ^ 5.0 5.1 5.2 5.3 Wells, D.G. The Penguin Dictionary of Curious and Interesting Geometry. Penguin book. Penguin Books. 1991. ISBN 9780140118131. LCCN 92131759.
- ^ Subramanian, Sai Ganesh and Eng, Mathew and Krishnamurthy, Vinayak and Akleman, Ergun, Delaunay Lofts: A New Class of Space-filling Shapes, ACM SIGGRAPH 2019 Posters, SIGGRAPH '19 (Los Angeles, California: ACM), 2019: 81:1––81:2, ISBN 978-1-4503-6314-3, doi:10.1145/3306214.3338576
- ^ Alam, S. M. Nazrul; Haas, Zygmunt J., Coverage and Connectivity in Three-dimensional Networks, Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MobiCom '06), New York, NY, USA: ACM: 346–357, 2006, ISBN 1-59593-286-0, arXiv:cs/0609069 , doi:10.1145/1161089.1161128.
- ^ Kepler, Johannes, The Six-Cornered Snowflake, Paul Dry Books, Footnote 18, p. 146, 2010, ISBN 9781589882850.
- ^ 9.0 9.1 Steinhaus 1999[4], pp. 185—190
- ^ 10.0 10.1 Wells 1991[5], pp. 233—234
- ^ Johnson, N. W. Uniform Polytopes. Cambridge, England: Cambridge University Press. 2000.
- ^ Counting polyhedra. numericana.com. [2016-01-10]. (原始内容存档于2016-05-06).
- ^ Grünbaum, B; Shephard, G. C. Tilings with Congruent Tiles. Bull. Amer. Math. Soc. 1980, 3 (3): 951–973 [2023-01-24]. doi:10.1090/s0273-0979-1980-14827-2 . (原始内容存档于2016-03-03).
- ^ Senechal, Marjorie, 7.2 The SCD (Schmitt–Conway–Danzer) tile, Quasicrystals and Geometry, Cambridge University Press: 209–213, 1996, ISBN 9780521575416.